കാറ്റലാൻ സംഖ്യ

സഞ്ചയനശാസ്ത്രത്തിലെ (combinatorics) ഒരു സംഖ്യാശ്രേണിയാണ് കാറ്റലാൻ സംഖ്യകൾ. സ്വാവർത്തനം ഉൾപ്പെടുന്ന അനവധി എണ്ണൽ പ്രശ്നങ്ങളിൽ ഈ സംഖ്യാശ്രേണി പ്രത്യക്ഷപ്പെടുന്നു. ബെൽജിയൻ ഗണിതശാസ്ത്രജ്ഞനായ യൂജീൻ ചാൾസ് കാറ്റലാന്റെ ബഹുമാനാർത്ഥമാണ് ഈ ശ്രേണിയുടെ നാമകരണം.
n-ആമത്തെ കാറ്റലാൻ സംഖ്യയെ ദ്വിപദ ഗുണാങ്കങ്ങളുടെ സഹായത്തോടെ ഇപ്രകാരം നിർവ്വചിക്കാം:
n=0,1,2,3… തുടങ്ങിയുള്ള ആദ്യത്തെ കാറ്റലാൻ സംഖ്യകൾ ഇവയാണ്:
- 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, ... (പൂർണ്ണസംഖ്യകളുടെ അനുക്രമങ്ങളുടെ ഓൺലൈൻ വിജ്ഞാനകോശത്തിലെ A000108 ശ്രേണി[1]).
ഗുണധർമ്മങ്ങൾ[തിരുത്തുക]
കാറ്റലാൻ സംഖ്യകളെ താഴെ കൊടുത്തിരിക്കുന്ന രീതിയിലും നിർവ്വചിക്കാം:
എന്ന സമവാക്യമുപയോഗിച്ചാൽ ഇത് ആമുഖത്തിലെ നിർവചനത്തിന് സമമാണെന്ന് കാണാം. കാറ്റലാൻ സംഖ്യകൾ എപ്പോഴും പൂർണ്ണസംഖ്യകളായിരിക്കും എന്ന് ഈ സൂത്രവാക്യം തെളിയിക്കുന്നു.
കാറ്റലാൻ സംഖ്യകൾ താഴെക്കൊടുത്തിരിക്കുന്ന ആവർത്തനബന്ധങ്ങൾ അനുസരിക്കുന്നു:
nന്റെ ഉയർന്ന വിലകൾക്ക് കാറ്റലാൻ സംഖ്യകളുടെ വളർച്ച ഇപ്രകാരമാണ്:
അതായത്, n അനന്തതയോടടുക്കുമ്പോൾ n-ആമത്തെ കാറ്റലാൻ സംഖ്യയുടെയും വലതുഭാഗത്തെ വ്യഞ്ജകത്തിന്റെയും അനുപാതത്തിന്റെ സീമ 1 ആണ്. ഫാക്റ്റോറിയലുകളുടെ സ്റ്റേർലിങ് ഏകദേശനം ഉപയോഗിച്ചും ജനകഫലനം ഉപയോഗിച്ചും ഇത് തെളിയിക്കാം.
n-ന്റെ വില രണ്ടിന്റെ ഒരു പൂർണ്ണ ഘാതത്തിൽ നിന്ന് ഒന്ന് കുറവാകുമ്പോൾ (n = 2k − 1) മാത്രമേ Cn ഒരു ഒറ്റസംഖ്യ ആകൂ, മറ്റെല്ലാ വിലകൾക്കും Cn ഇരട്ടസംഖ്യ ആയിരിക്കും. മാത്രമല്ല, C2 = 2, C3 = 5 എന്നിവ മാത്രമാണ് അഭാജ്യമായ കാറ്റലാൻ സംഖ്യകൾ.[2]
കാറ്റലാൻ സംഖ്യകളെ സമാകലനം വഴിയും നിർവചിക്കാം
ഇവിടെ ഹൗസ്ഡോർഫ് ആഘൂർണ പ്രശ്നത്തിന്റെ [0, 4] ഇടവേളയിലെ നിർദ്ധാരണമാണ് കാറ്റലാൻ സംഖ്യകൾ എന്നതിനാലാണിത്.
സഞ്ചയനശാസ്ത്രം[തിരുത്തുക]
സഞ്ചയനശാസ്ത്രത്തിലെ അനവധി എണ്ണൽ പ്രശ്നങ്ങളുടെ നിർദ്ധാരണത്തിൽ കാറ്റലാൻ സംഖ്യകൾ പ്രത്യക്ഷപ്പെടുന്നു. റിച്ചാർഡ് പി. സ്റ്റാൻലിയുടെ Enumerative Combinatorics എന്ന പുസ്തകത്തിന്റെ രണ്ടാം വാള്യത്തിലെ അഭ്യാസങ്ങളിൽ കാറ്റലാൻ സംഖ്യകളുടെ 66 വ്യാഖ്യാനങ്ങളുണ്ട്.[3] ചില ഉദാഹരണങ്ങൾ C3 = 5, C4 = 14 എന്നിവയുടെ സ്പഷ്ടീകരണത്തോടൊപ്പം വിശദീകരിക്കുന്നു:

- 2n നീളമുള്ള ഡൈക്ക് വാക്കുകളുടെ എണ്ണം Cn ആണ്[4]: n Xകളും n Yകളും ഉള്ളതും തുടക്കം മുതൽ എണ്ണുകയാണെങ്കിൽ ഒരുവേളയിലും Xകളെക്കാൾ Yകൾ ഇല്ലാത്തതുമായ അക്ഷരശൃംഖലയാണ് ഡൈക്ക് വാക്ക്. ആറ് അക്ഷരങ്ങളുള്ള ഡൈക്ക് വാക്കുകൾ ഇവയാണ്:
- ഡൈക്ക് വാക്കുകളിലെ X-നെ തുറക്കുന്ന വലയവും Y-നെ അടയ്ക്കുന്ന വലയവുമായി വ്യാഖ്യാനിക്കുകയാണെങ്കിൽ, ജോഡികൾ ശരിയായുള്ള n ജോഡി വലയങ്ങളുടെ എണ്ണം Cn ആണ്:
- n + 1 ഘടകങ്ങളെ ക്രമം മാറ്റാതെ ജോഡികളായി വലയങ്ങളിലാക്കാനുള്ള രീതികളുടെ എണ്ണം. ഇത്രയും സങ്കാര്യങ്ങളുടെ മേൽ ഗുണനം പോലുള്ള ഏതെങ്കിലും ദ്വയാങ്കസംക്രിയ പടിപടിയായി നടത്താനുള്ള രീതികളുടെ എണ്ണത്തിന് തുല്യമാണിത്. ഉദാഹരണമായി, n = 3 ആണെങ്കിൽ abcd യെ C3 = 5 രീതിയിൽ നിർദ്ധരിക്കാം:

- ദ്വയാങ്കസംക്രിയ പടിപടിയായി നടത്തുന്നതിനെ ഒരു പൂർണ്ണ ബൈനറി ട്രീ ആയി പ്രതിനിധീകരിക്കാം (മൂലം നിർണ്ണയിച്ചതും ഓരോ ശീർഷത്തിനും പൂജ്യം അഥവാ രണ്ട് പിൻഗാമികളുള്ളതുമായ ബൈനറി ട്രീയെയാണ് പൂർണ്ണം എന്ന് വിളിക്കുന്നത്). അതിനാൽ n + 1 ലീഫുകളുള്ള പൂർണ്ണ ബൈനറി ട്രീകളുടെ എണ്ണവും Cn ആണ്:

- n + 1 ശീർഷങ്ങളുള്ള സമരൂപമല്ലാത്ത ക്രമാനുസാര (ordered) ട്രീകളുടെ എണ്ണം Cn ആണ്. ഓരോ ശീർഷത്തിന്റെയും പിൻഗാമികൾക്ക് ഇടത്തുനിന്ന് വലത്തോട്ടേക്കുള്ള ക്രമം നിശ്ചയിച്ചിട്ടുള്ളതും മൂലമുള്ളതുമായ (rooted) ട്രീകളാണ് ക്രമാനുസാരം.
- ഒരു ജാലികയിൽ (0,0) എന്ന ബിന്ദുവിൽ നിന്നും (n,n) എന്ന ബിന്ദുവിലേക്കുള്ള ഏകതാനമായ പഥങ്ങളിൽ വികർണ്ണത്തിന് മുകളിൽ പോകാത്തവയുടെ എണ്ണം Cn ആണ്. മുകളിലേക്കും വലത്തേക്കുമുള്ള വക്കുകൾ മാത്രമടങ്ങിയ പഥങ്ങളെയാണ് ഏകതാനം (monotonic) എന്ന് വിളിക്കുന്നത്. n = 4 നുള്ള ഇത്തരം C4 = 14 പഥങ്ങൾ താഴെക്കൊടുക്കുന്നു:

പഥത്തിലെ ഓരോ കോളത്തിന്റെയും ഉയരങ്ങൾ കൊണ്ടും ഇവയെ സംക്ഷിപ്തമായി പ്രതിനിധീകരിക്കാം:[5]

- n + 2 വശങ്ങളുള്ള അവകല ബഹുഭുജങ്ങളെ പരസ്പരം വിച്ഛേദിക്കാത്ത വികർണ്ണങ്ങൾ കൊണ്ട് n ത്രികോണങ്ങളാക്കി മുറിക്കാനുള്ള രീതികളുടെ എണ്ണവും Cn ആണ്. ഷഡ്ഭുജങ്ങളെ നാല് ത്രികോണങ്ങളായി C4 = 14 രീതിയിൽ ഭാഗിക്കാം:

- സ്റ്റാക്ക് ഉപയോഗിച്ച് ക്രമത്തിലാക്കാവുന്ന {1, ..., n} ന്റെ ക്രമചയങ്ങളുടെ എണ്ണം. 231 എന്ന ക്രമചയക്രമം അടങ്ങിയിട്ടില്ലാത്ത ക്രമചയങ്ങളെയാണ് ഇങ്ങനെ സ്റ്റാക്ക് മാത്രം ഉപയോഗിച്ച് ക്രമത്തിലാക്കാൻ സാധിക്കുക.
- 231 മാത്രമല്ല, മൂന്ന് അംഗങ്ങളുള്ള മറ്റേത് ക്രമചയക്രമെടുത്താലും അത് അടങ്ങിയിട്ടില്ലാത്ത ക്രമചയങ്ങളുടെ എണ്ണം Cn ആണ്. ഉദാഹരണമായി, 123 എന്ന ക്രമചയക്രമം (അതായത്, ആരോഹണക്രമത്തിലുള്ള മൂന്ന് സംഖ്യകൾ) ഇല്ലാത്ത n = 4 ന്റെ ക്രമചയങ്ങൾ C4 = 14 എണ്ണമുണ്ട്: 1432, 2143, 2413, 2431, 3142, 3214, 3241, 3412, 3421, 4132, 4213, 4231, 4312, 4321 എന്നിവയാണിവ.
- {1, ..., n} എന്ന ഗണത്തിന്റെ പരസ്പരം മുറിച്ചുകടക്കാത്ത (non-crossing) വിഭജനങ്ങളുടെ (partition) എണ്ണം Cn ആണ്. ഗണത്തിന്റെ ആകെ വിഭജനങ്ങളുടെ എണ്ണം n-ആമത്തെ ബെൽ സംഖ്യ ആയതിനാൽ, ഓരോ കാറ്റലാൻ സംഖ്യയും അതിന്റെ യോജിച്ച ബെൽ സംഖ്യയെക്കാൾ വലുതാകാൻ സാധിക്കില്ലെന്ന് വരുന്നു. ഓരോ ബ്ലോക്കിന്റെയും വലിപ്പം 2 ആയുള്ള {1, ..., 2n} ഗണത്തിന്റെ പരസ്പരം മുറിച്ചുകടക്കാത്ത വിഭജനങ്ങളുടെ എണ്ണവും Cn തന്നെ.
- n പടികളുള്ള ഒരു പടിക്കെട്ടിന്റെ രൂപം n ചതുരങ്ങളുപയോഗിച്ച് പാവാനുള്ള രീതികളുടെ എണ്ണം. n = 4 ഉദാഹരണമായെടുക്കാം:

- ഒരു തിരച്ഛീനരേഖയിൽ നിന്ന് തുടങ്ങി ഒരിക്കലും ആ രേഖയ്ക്ക് താഴേക്ക് പോകാത്ത വിധത്തിൽ മുകളിലേക്കുള്ള n വരകളും താഴേക്കുള്ള n വരകളുമുപയോഗിച്ച് നിർമ്മിക്കാവുന്ന "പർവ്വതനിരകളുടെ" എണ്ണം.
| * | 1 way | |
| /\ | 1 way | |
| /\ /\/\,/\ |
2 ways | |
| /\ /\/\/\/\/\ /\/\/\,/\/\,/\/\,/\,/\ |
5 ways |
- 2×n ഡയഗ്രം ഉള്ള യങ് ടാബ്ലോകളുടെ എണ്ണം. അതായത്, ഓരോ വരിയും നിരയും ആരോഹണക്രമത്തിൽ വരുന്ന തരത്തിൽ ഒരു 2×n പട്ടിക 1, 2, ..., 2n എന്ന സംഖ്യകൾ കൊണ്ട് നിറയ്ക്കാനുള്ള രീതികളുടെ എണ്ണം.
- 2n വക്കുകളുള്ള ഒരു അവകല ബഹുഭുജത്തിന്റെ ശീർഷങ്ങളെ പരസ്പരം മുറിച്ചുകടക്കാത്ത n ജോഡികളായി യോജിപ്പിക്കാനുള്ള രീതികളുടെ എണ്ണം.
- ലേബൽ ചെയ്യാത്ത n വസ്തുക്കളുടെ സെമി-ഓർഡറുകളുടെ എണ്ണം.[6]
- കെമിക്കൽ എൻജിനീയറിംഗിൽ: n ഘടകങ്ങളുള്ള ഒരു മിശ്രിതത്തെ അതിന്റെ ഘടകഭാഗങ്ങളാക്കി മാറ്റാനുതകുന്ന വിശ്ലേഷപരമ്പരകളുടെ എണ്ണം.[7]
സൂത്രവാക്യത്തിന്റെ തെളിവ്[തിരുത്തുക]
മേലെ കൊടുത്തിരിക്കുന്ന എണ്ണൽ പ്രശ്നങ്ങളുടെ നിർദ്ധാരണത്തിന്
എന്ന സൂത്രവാക്യം ഉപയോഗിക്കാം എന്നത് പല രീതിയിലും തെളിയിക്കാം. ജനകഫലനങ്ങൾ ഉപയോഗിച്ചുള്ള തെളിവുകളും ഉഭയക്ഷേപ (bijective) തെളിവുകളും (ഒരു കൂട്ടം വസ്തുക്കളെ രണ്ടു രീതിയിൽ എണ്ണി ആ എണ്ണങ്ങളുടെ വ്യഞ്ജകങ്ങളുടെ തുല്യത സ്ഥാപിക്കുന്ന തെളിവുകൾ) ഈ സൂത്രവാക്യത്തിനുണ്ട്.
ജനകഫലനം[തിരുത്തുക]
മേൽ വിവരിച്ച എണ്ണൽ പ്രശ്നങ്ങളെല്ലാം സെഗ്നറുടെ[8] ആവർത്തനബന്ധം ഉപയോഗിക്കുന്നു എന്ന നിരീക്ഷണമാണ് ആദ്യത്തെ പടി
ഉദാഹരണമായി, w എന്നത് രണ്ടിലധികം അക്ഷരങ്ങളുള്ള ഒരു ഡൈക്ക് വാക്കാണെങ്കിൽ അതിനെ ഒറ്റ രീതിയിൽ താഴെക്കൊടുത്തിരിക്കുന്ന രൂപത്തിൽ എഴുതാൻ സാധിക്കും:
- w = Xw1Yw2
ഇവിടെ w1, w2 എന്നിവ (ഒരുപക്ഷെ ശൂന്യമായ) ഡൈക്ക് വാക്കുകളാണ്. കാറ്റലാൻ സംഖ്യകളുടെ ജനകഫലനത്തിന്റെ നിർവചനമെടുക്കുക
സെഗ്നറുടെ ആവർത്തനബന്ധത്തിന്റെ ഇരുഭാഗവും ഘാതശ്രേണികൾ ഉപയോഗിച്ച് വികസിപ്പിച്ചാൽ ജനകഫലനത്തിന്റെ ഈ സമവാക്യം ലഭിക്കുന്നു:
ഈ സമവാക്യം ബീജഗണിതമുപയോഗിച്ച് നിർദ്ധരിക്കാം
പൂജ്യത്തിനു ചുറ്റും ഈ നിർദ്ധാരണത്തിന്റെ ഘാതശ്രേണി കണക്കാക്കാൻ സാധിക്കും. കാറ്റലാൻ സംഖ്യകളുടെ ജനകഫലനത്തിന്റെ ഘാതശ്രേണിയായതിനാൽ ഇതിന്റെ ഗുണാങ്കങ്ങൾ കാറ്റലാൻ സംഖ്യകളായിരിക്കണം. വർഗ്ഗമൂലത്തെ ഒരു ഘാതശ്രേണിയായി വികസിപ്പിക്കാൻ ഈ അനന്യത ഉപയോഗിക്കാം
ന്യൂട്ടന്റെ ദ്വിപദപ്രമേയത്തിന്റെ സാമാന്യവൽക്കരണമുപയോഗിച്ചും അവകലജങ്ങൾ കണ്ടുപിടിച്ച് ടെയ്ലർ ശ്രേണി ഉപയോഗിച്ചും ഇത് തെളിയിക്കാം. ഈ സൂത്രവാക്യത്തിൽ y = −4x എന്നു തിരുത്തി c(x) ന്റെ നിർദ്ധാരണത്തിൽ ഉൾപ്പെടുത്തുകയും n ന്റെ വിലയിൽ 1 മാറ്റം വരുത്തുകയും ചെയ്താൽ
എന്ന് ലഭിക്കുന്നു. ഈ വ്യഞ്ജകത്തിന്റെ ഗുണാങ്കങ്ങൾ കാറ്റലാൻ സംഖ്യകളായതിനാൽ Cnനുള്ള ഉദ്ദേശിച്ച സൂത്രവാക്യം ലഭിച്ചിരിക്കുന്നു.
ഉഭയക്ഷേപം[തിരുത്തുക]
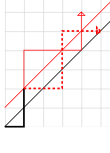
ബെർട്രാന്റിന്റെ ബാലറ്റ് പ്രശ്നം നിർദ്ധരിക്കാനായി ആദ്യം ഉപയോഗിച്ച ആന്ദ്രേയുടെ പ്രതിഫലന സൂത്രം അടിസ്ഥാനമാക്കിയാണ് ഈ തെളിവ് (ദെസിരെ ആന്ദ്രേയുടെ പേരിലാണറിയപ്പെടുന്നതെങ്കിലും ഈ രീതി കണ്ടെത്തിയത് ഏബ്ലിയും മിറിമാനോഫുമാണ്[9]).
n × n ജാലികയുടെ വികർണ്ണത്തിൽ തുടങ്ങുകയും അവസാനിക്കുകയും ചെയ്യുന്ന പഥങ്ങൾ എണ്ണിത്തിട്ടപ്പെടുത്താം. ഓരോ പഥത്തിലും വലത്തേക്കും മുകളിലേക്കും n വീതം ചുവടുകളുണ്ട്. ആകെയുള്ള 2n ചുവടുകളിൽ ഏതൊക്കെ വലത്തോട്ടും മുകളിലേക്കും എടുക്കണമെന്നുള്ളത് നമുക്ക് സ്വതന്ത്രമായി തീരുമാനിക്കാമെന്നതിനാൽ ആകെ ഏകതാനമായ പഥങ്ങളുണ്ടെന്ന് വരുന്നു. അസാധുവായ ഓരോ പഥവും വികർണ്ണം മുറിച്ചുകടന്ന് അതിനു തൊട്ടുമുകളിലായി സമാന്തരമായുള്ള രേഖയിലെത്തുന്നു (ചിത്രത്തിലെ ചുവന്ന മുറിയാത്ത വരകൾ). അതിനുശേഷമുള്ള പഥത്തിന്റെ ഭാഗം ഈ രേഖയ്ക്കു (ഇതിനെ നിർണ്ണായക രേഖ എന്നു വിളിക്കാം) കുറുകെ പ്രതിഫലിപ്പിക്കാം (ചുവന്ന മുറിഞ്ഞ വരകൾ). മുകളിലേക്കും വലത്തോട്ടുമുള്ള ചുവടുകളെ പരസ്പരം മാറ്റുന്നതിന് തുല്യമാണിത്. പഥത്തിന്റെ പ്രതിഫലിപ്പിക്കാത്ത ഭാഗത്ത് വലത്തോട്ടുള്ളതിനെക്കാൾ മുകളിലേക്ക് ഒരു ചുവട് കൂടുതലുണ്ടായിരുന്നു, അതിനുശേഷമുള്ള ഭാഗത്ത് ഒരു ചുവട് കുറവും. രണ്ടാമത്തെ ഭാഗം പ്രതിഫലിപ്പിക്കുമ്പോൾ മുകളിലേക്ക് വലത്തോട്ടുള്ളതിനെക്കാൾ ആകെ രണ്ട് ചുവടുകൾ അധികമുണ്ടെന്നു വരുന്നു. അതായത്, മുകളിലേക്ക് ആകെ n + 1 ചുവടുകളും വലത്തേക്ക് ആകെ n - 1ഉം. പ്രതിഫലിപ്പിച്ച ശേഷം പഥം അതിനാൽ അവസാനിക്കുക (n − 1, n + 1) എന്ന ബിന്ദുവിലാണ്. ഈ ബിന്ദുവിൽ അവസാനിക്കുന്ന എല്ലാ പഥങ്ങളും നിർണ്ണായകരേഖ മുറിച്ചുകടക്കണം എന്നതിനാൽ അസാധുവായ പഥങ്ങൾക്കും (n − 1, n + 1)ൽ അവസാനിക്കുന്ന പഥങ്ങൾക്കുമിടയിൽ ഒരു ഉഭയക്ഷേപം ലഭിക്കുന്നു. അസാധുവായ പഥങ്ങളുടെ എണ്ണം അതിനാൽത്തന്നെ
ആണെന്നു വരുന്നു. ആകെ പഥങ്ങളുടെ എണ്ണത്തിൽ നിന്ന് ഈ സംഖ്യ കുറച്ചാൽ കാറ്റലാൻ പഥങ്ങളുടെ എണ്ണം ലഭിക്കുന്നു
ഇങ്ങനെ ഉഭയക്ഷേപമുപയോഗിച്ചും കാറ്റലാൻ സംഖ്യകളുടെ സൂത്രവാക്യം കണ്ടുപിടിക്കാം. ഇതിനുപുറമെ ജാലികയിലെ പഥങ്ങളുപയോഗിച്ചും ഡൈക്ക് വാക്കുകളുപയോഗിച്ചും മറ്റനേകം ഉഭയക്ഷേപ തെളിവുകളുണ്ട്.
ഹാൻകെൽ മാട്രിക്സ്[തിരുത്തുക]
(i, j)ആമത്തെ സംഖ്യ Ci+j−2 എന്ന കാറ്റലാൻ സംഖ്യയായുള്ള n×n സമചതുര മാട്രിക്സിന്റെ സാരണികം എപ്പോഴും 1 ആയിരിക്കും. ഇത് ഒരുതരം ഹാൻകെൽ മാട്രിക്സ് ആണ്. ഉദാഹരണമായി, n = 4 ആകുമ്പോൾ
ഇതിനു പകരം (i, j) ആമത്തെ സംഖ്യ Ci+j−1 ആക്കിയാലും സാരണികം എല്ലായ്പ്പോഴും 1 തന്നെ ആയിരിക്കും. n = 4 ആകുമ്പോൾ
ഈ രണ്ട് നിബന്ധനകൾ ഉപയോഗിച്ചും കാറ്റലാൻ സംഖ്യകളെ നിർവചിക്കാം.
ചരിത്രം[തിരുത്തുക]

ബഹുഭുജങ്ങളെ ത്രികോണങ്ങളാക്കി മുറിക്കുന്നതിനെക്കുറിച്ച് പഠിക്കവെ ലെയനാർഡ് ഓയ്ലർ പതിനെട്ടാം നൂറ്റാണ്ടിൽ കാറ്റലാൻ ശ്രേണി വിവരിച്ചു. ഹാനോയ് ഗോപുരപ്രശ്നത്തെക്കുറിച്ചുള്ള ഗവേഷണത്തിനിടയിൽ ഈ സംഖ്യകൾക്ക് വലയങ്ങളുള്ള വ്യഞ്ജകങ്ങളുമായുള്ള ബന്ധം കണ്ടെത്തിയ യൂജീൻ ചാൾസ് കാറ്റലാന്റെ പേരിലാണ് ശ്രേണി അറിയപ്പെടുന്നത്. 1887-ൽ ഡീ. ആന്ദ്രേ ആണ് ഡൈക്ക് വാക്കുകളെ എണ്ണാൻ കാറ്റലാൻ സംഖ്യകൾ ഉപയോഗിക്കാമെന്ന് മനസ്സിലാക്കിയത്.
മംഗോളിയൻ ഗണിതശാസ്ത്രജ്ഞനായ മിങ് ആൻ തു 1730-ൽ തന്നെ ചൈനയിൽ കാറ്റലാൻ ശ്രേണി ഉപയോഗിച്ചിരുന്നു എന്ന് 1988-ൽ വെളിവായി..[10][11] അദ്ദേഹം തുടങ്ങിവച്ച ഗെ യുവാൻ മി ലു ജീ ഫ (വൃത്തത്തെ ഭാഗിക്കാനുള്ള കൃത്യമായ അനുപാതം പെട്ടെന്ന് കണ്ടുപിടിക്കാനുള്ള രീതി) എന്ന ഗ്രന്ഥം പിന്നീട് ശിഷ്യനായ ചെൻ ജിക്സിൻ 1774-ൽ പൂർത്തിയാക്കുകയും അതിനും അറുപതു വർഷം കഴിഞ്ഞ് പ്രസിദ്ധീകരിക്കുകയുമായിരുന്നു. sin(2α), sin(4α) എന്നിവയെ sin(α) യുടെ ശ്രേണിയായി വിവരിക്കാൻ അദ്ദേഹം കാറ്റലാൻ സംഖ്യകൾ ഉപയോഗിച്ചു.
അവലംബം[തിരുത്തുക]
- ↑ "കാറ്റലാൻ സംഖ്യകൾ". പൂർണ്ണസംഖ്യകളുടെ അനുക്രമങ്ങളുടെ ഓൺലൈൻ വിജ്ഞാനകോശം. Retrieved 2018 ഡിസംബർ 2.
{{cite web}}: Check date values in:|access-date=(help) - ↑ Koshy, Thomas; Salmassi, Mohammad (2006). Parity and primality of Catalan numbers. The Mathematical Association of America.
- ↑ Stanley, Richard P. (2015), Catalan numbers. Cambridge University Press, ISBN 978-1-107-42774-7
- ↑ "Equivalent definitions of Dyck paths". Archived from the original on 2020-12-03. Retrieved 2018-12-02.
- ↑ Črepinšek, Matej; Mernik, Luka (2009). "An efficient representation for solving Catalan number related problems" (PDF). International Journal of Pure and Applied Mathematics. 56 (4): 589–604.
- ↑ Kim, K. H.; Roush, F. W. (1978), "Enumeration of isomorphism classes of semiorders", Journal of Combinatorics, Information &System Sciences, 3 (2): 58–61, MR 0538212.
- ↑ Thompson, R. W.; King, C. J. (1972), "Systematic synthesis of separation schemes", American Institution of Chemical Engineers Journal, 18 (5): 941–948, doi:10.1002/aic.690180510.
- ↑ A. de Segner, Enumeratio modorum, quibus figurae planae rectilineae per diagonales dividuntur in triangula. Novi commentarii academiae scientiarum Petropolitanae 7 (1758/59) 203–209.
- ↑ Renault, Marc, Lost (and found) in translation: André's actual method and its application to the generalized ballot problem. Amererican Mathematical Monthly 115 (2008), no. 4, 358–363.
- ↑ The 18th century Chinese discovery of the Catalan numbers
- ↑ "Ming Antu, the First Inventor of Catalan Numbers in the World". Archived from the original on 2020-01-31. Retrieved 2018-12-02.
























