സമഭുജത്രികോണം

ഇംഗ്ലീഷ് വിലാസം

http://ml.wikipedia.org/wiki/Equilateral_triangle

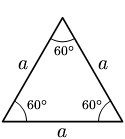
മൂന്നു വശങ്ങളും മൂന്നു കോണളവുകളും തുല്യമായ ത്രികോണങ്ങളാണ് സമഭുജ ത്രികോണങ്ങൾ. ആയതിനാൽ ഓരോ കോണളവും 60 ഡിഗ്രീ വീതമായിരിയ്ക്കും.

ഒരു വശം $a\,$യും ലംബശീർ‌ഷം $h\,$ഉം തന്നിരുന്നാൽ സമഭുജത്രികോണത്തിന്റെ വിസ്തീർ‌ണ്ണം കാണുന്നതിന് $\frac{1}{2} ah\,$ എന്ന സൂത്രവാക്യം ഉപയോഗിയ്ക്കുന്നു.

$a\,$ വശമായുള്ള സമഭുജത്രികോണം ആധാരമാക്കി വരയ്ക്കുന്ന:

• $r\,$ ആരമായുള്ള അന്തർ‌വൃത്തത്തിന്റെ വിസ്തീർ‌ണ്ണം $\pi r^2\,$ അഥവാ $\frac{1}{12} \pi a^2\,$ എന്ന സൂത്രവാക്യം ഉപയോഗിച്ചും
• $R\,$ ആരമായുള്ള പരിവൃത്തത്തിന്റെ വിസ്തീർ‌ണ്ണം $\pi R^2\,$ അഥവാ $\frac{1}{3} \pi a^2$ എന്ന സൂത്രവാക്യം ഉപയോഗിച്ചും കണ്ടെത്താം.

നിർ‌മ്മിതി

സമഭുജ ത്രികോണത്തിന്റെ നിർമ്മിതി

ആരമായുള്ള ഒരു വൃത്തം നിർ‌മിയ്ക്കുക. ഇതേ ആരത്തിൽ തന്നെ കോം‌പസ്സുപയോഗിച്ച് വേറൊരു വൃത്തം നിർമ്മിച്ച്, വൃത്തകേന്ദ്രങ്ങളേയും വൃത്തങ്ങൾ തമ്മിൽ സന്ധിയ്ക്കുന്ന ബിന്ദുക്കളേയും യോജിപ്പിച്ചാൽ സമഭുജത്രികോണം ലഭിയ്ക്കും.