വൃത്തം
വിക്കിപീഡിയ, ഒരു സ്വതന്ത്ര വിജ്ഞാനകോശം.
| വൃത്തം എന്ന വാക്കാല് വിവക്ഷിക്കാവുന്ന ഒന്നിലധികം കാര്യങ്ങളുണ്ട്. അവയെക്കുറിച്ചറിയാൻ വൃത്തം (നാനാര്ത്ഥങ്ങള്) എന്ന താള് കാണുക. |  |
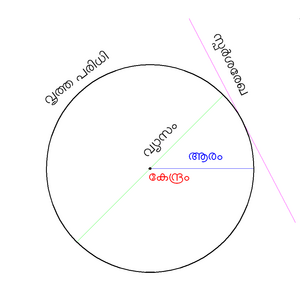
ഒരു ദ്വിമാനതലത്തിലെ കേന്ദ്രബിന്ദുവില് നിന്ന് നിശ്ചിത ദൂരത്തില് അതേ തലത്തില് നിലകൊള്ളുന്ന എല്ലാ ബിന്ദുക്കളുടേയും ഗണത്തെ പ്രതിനിധീകരിക്കുന്ന ജ്യാമിതീയ രൂപമാണ് വൃത്തം. ഒരു തലത്തില് സ്ഥിതി ചെയ്യുന്ന വശങ്ങളില്ലാത്ത ഏക ജ്യാമിതീയ രൂപമാണ് വൃത്തം.വൃത്തം എന്ന പദം പലപ്പോഴും വക്രതയിലുള്ള ബിന്ദുക്കളെ സൂചിപ്പിയ്ക്കുന്നതിലുപരിയായി വൃത്തപരിധിയ്ക്കുള്ളിലെ തലത്തെയാണ് വിവരിയ്ക്കുന്നത്.ഏറ്റവും കുറഞ്ഞ ചുറ്റളവില് ഏറ്റവും കൂടിയ ഉപരിതല വിസ്തീര്ണ്ണം ഈ രൂപത്തിന്റെ മറ്റൊരു പ്രത്യേകതയാണ്. ഈ ഒരു പ്രത്യേകതയാണ് കിണറിന്റെ ആകൃതി വൃത്തത്തില് ആകുന്നത്.
ദ്വിതല യൂലീഡിയന് രൂപമാണ് വൃത്തം.വൃത്തം കോണികങ്ങള് എന്ന വിഭാഗത്തില് ഉള്പ്പെടുന്നു.ഒരു വൃത്തസ്തൂപിക അതിന്റെ അക്ഷത്തിന് ലംബമായ തലവുമായി യോജിയ്ക്കുമ്പോഴാണ് വൃത്തം ഉണ്ടാകുന്നത്.ഇപ്രകാരം r ആരവും (h,k) കേന്ദ്രവുമായ വൃത്തത്തിന്റെ (x – h)2 + (y - k)2 = r2 എന്ന സമവാക്യം ലഭിയ്ക്കുന്നു.ദീര്ഘവൃത്തത്തിന്റെ ഒരു പ്രത്യേകരൂപമാണ് വൃത്തം.
വൃത്തകേന്ദ്രത്തില് നിന്നും വൃത്തപരിധിയിലുള്ള ഏതൊരു ബിന്ദുവിലേയ്ക്കുമുള്ള അകലം തുല്യമായിരിയ്ക്കും.
ഉള്ളടക്കം |
[തിരുത്തുക] ആരം
കേന്ദ്രബിന്ദുവില് നിന്ന് വൃത്തത്തിലെ ഏതൊരു ബിന്ദുവിലേക്കും ഉള്ള ദൂരത്തെ ആരം എന്നു പറയുന്നു. വൃത്തപരിധിയും വിസ്തീര്ണ്ണവും ആരത്തെ അടിസ്ഥാനാമാക്കിയാണ് നിര്ണ്ണയിയ്ക്കുന്നത്.
[തിരുത്തുക] വ്യാസം
വൃത്തത്തിലെ രണ്ടു ബിന്ദുക്കള് കൂട്ടി യോജിപ്പിക്കുമ്പോഴുണ്ടാകുന്ന രേഖാഖണ്ഡം അതിന്റെ കേന്ദ്രത്തിലൂടെ കടന്നു പോകുന്നുവെങ്കില് ആ രേഖാഖണ്ഡത്തിനെ നീളത്തെ വ്യാസം എന്നു പറയുന്നത്.
[തിരുത്തുക] ഞാണ്
ഒരു വൃത്തത്തിലെ ഏതെങ്കിലും ഒരു ബിന്ദുവില് ആരംഭിച്ച് അതേ വൃത്തത്തിലെ മറ്റൊരു ബിന്ദുവില് അവസാനിക്കുന്ന രേഖയെ ഞാണ് എന്നു വിളിക്കുന്നു. ഒരു വൃത്തത്തിലെ ഏറ്റവും നീളമേറിയ ഞാണ് അതിന്റെ വ്യാസമാണ്.
[തിരുത്തുക] ചാപം
വൃത്തപരിധിയുടെ ഒരു ഭാഗത്തേയാണ് ചാപം എന്ന് പറയുന്നത്.വൃത്തചാപം ഡിഗ്രിയിലാണ് പറയുന്നത്.
[തിരുത്തുക] വൃത്തപരിധിയും വിസ്തീര്ണ്ണവും
വൃത്തത്തിന്റെ വക്രതയുടെ അതിര്ത്തിയെയാണ് വൃത്തപരിധി കൊണ്ട് ഉദ്ദേശിയ്ക്കുന്നത്.അതിര്ത്തിയുടെ നീളമാണ് വൃത്തപരിധിയുടെ അളവ്.വൃത്തപരിധിയെ 360തുല്യഡിഗ്രിയാക്കി ഭാഗിച്ചിരിയ്ക്കുന്നു.വൃത്തപരിധിയും വ്യാസവും തമ്മിലുള്ള അംശബന്ധമാണ് പൈ,ഇതിന്റെ അളവാണ് 3.14159265.ദ്വിമാനതലത്തില് തുല്യചുറ്റളവുള്ള ഏതൊരു രൂപത്തേക്കാളം വിസ്തീര്ണ്ണം കൂടുതല് വൃത്തത്തിനാണ്.
[തിരുത്തുക] സൂത്രവാക്യം
- വൃത്തപരിധിയുടെ നീളം(C) അളക്കുന്നതിനുള്ള സൂത്രവാക്യം:-
r = ആരം, π പൈ = 3.1415926[1]
- വൃത്തത്തിന്റെ വിസ്തീര്ണ്ണം(A) അളക്കുന്നതിനുള്ള സൂത്രവാക്യം:-
 വൃത്തപരിധി |
[തിരുത്തുക] അവലംബം
ഈ ലേഖനവുമായി ബന്ധപ്പെട്ട കൂടുതല് പ്രമാണങ്ങള് ലഭ്യമാണ്
 |
ജ്യാമിതിയുമായി ബന്ധപ്പെട്ട ഈ ലേഖനം അപൂര്ണ്ണമാണ്. ഇത് പൂര്ത്തിയാക്കാന് സഹകരിക്കുക. സഹായത്തിനു ഈ ലേഖനത്തിന്റെ ഇംഗ്ലീഷ് പതിപ്പ്. |
