കുതിര സഞ്ചാരം
 |
 |
 |
 |
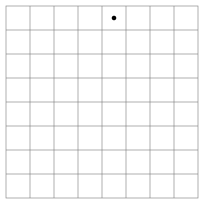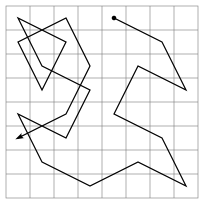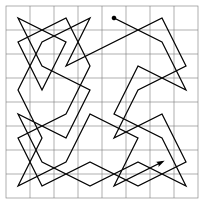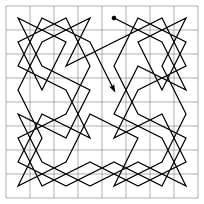
ചെസ്സ് പലകയിലെ കുതിരയെ അടിസ്ഥാനമാക്കിയ ഒരു ഗണിതശാസ്ത്രപ്രശ്നമാണ് കുതിര സഞ്ചാരം (Knight's tour). ഒഴിഞ്ഞ ചെസ്സ് പലകയിൽ ഒരു കുതിരയെ വെക്കുകയും, ചെസ്സിലെ നിയമങ്ങളനുസരിച്ച് പലകയിലെ എല്ലാ കളങ്ങളിലും ഒരിക്കൽ മാത്രം ചാടിക്കണമെന്നതുമാണ് പ്രശ്നം. കുതിരയുടെ സഞ്ചാരം തുടങ്ങിയേടത്തു തന്നെ അവസാനിക്കുകയാണെങ്കിൽ അതിനെ അടഞ്ഞ സഞ്ചാരം (Closed tour) എന്നു വിളിക്കുന്നു. അങ്ങനെയാകുന്നില്ലെങ്കിൽ അതിനെ തുറന്ന സഞ്ചാരം (Open tour) എന്നും വിളിക്കുന്നു. ആകെ ലഭ്യമായ തുറന്ന സഞ്ചാരങ്ങളുടെ എണ്ണം ഇന്നും അജ്ഞാതമാണ്. കുതിര സഞ്ചാര പ്രശ്നം പരിഹരിക്കുന്ന പ്രോഗ്രാം എഴുതുന്ന ചോദ്യം കമ്പ്യൂട്ടർ ശാസ്ത്ര വിദ്യാർത്ഥികൾക്കു സാധാരണയായി ലഭിക്കുന്ന ചോദ്യങ്ങളിലൊന്നാണ്[1]. വിവിധ രീതിയിലുള്ള ചെസ്സ് പലകകളുപയോഗിച്ച് ഈ പ്രശ്നം ചെയ്യാറുണ്ട്. 8 × 8 എന്ന സാധാരണ ചെസ്സ് പലകക്കു പുറമെ മറ്റു പല രീതിയിലുള്ള ചെസ്സ് പലകകളിലും ഇത് ചെയ്യാറുണ്ട്.
സിദ്ധാന്തം[തിരുത്തുക]
ഗ്രാഫ് സിദ്ധാന്തത്തിലെ ഹാമിൽട്ടോണിയൻ പാത പ്രശ്നത്തിന്റെ ഒരു ഉദാഹരണമാണ് കുതിര സഞ്ചാരം. അടഞ്ഞ സഞ്ചാരത്തിന്റെ നിർദ്ധാരണത്തിലെത്തുന്നത് ഹാമിൽട്ടോണിയൻ ചക്ര പ്രശ്നത്തിന്റെ ഒരു ഉദാഹരണവുമാണ്. പക്ഷേ, ഹാമിൽട്ടോണിയൻ പാത പ്രശ്നത്തിനു വിപരീതമായി ഇവിടെ പ്രശ്നത്തിന്റെ നിർദ്ധാരണം ലീനിയർ ടെമിൽ[2] ചെയ്യാൻ സാദ്ധ്യമാണ്.
ചരിത്രം[തിരുത്തുക]
കുതിര സഞ്ചാര പ്രശ്നത്തിന്റെ ആദ്യ പ്രതിപാദ്യമുള്ളത് ഒമ്പതാം നൂറ്റാണ്ടിൽ ജീവിച്ചിരുന്ന കാശ്മീരി കവിയായ രുദ്രടൻ എഴുതിയ കാവ്യാലങ്കാര[3] എന്ന ഗ്രന്ഥത്തിലെ ഒരു ശ്ലോകത്തിലാണ്.
അവലംബം[തിരുത്തുക]
- ↑ H. M. Deitel, P. J. Deitel. "Java How To Program Fifth Edition." Prentice Hall, Upper Saddle River, New Jersey, pp. 326-328. 2003.
- ↑ A. Conrad, T. Hindrichs, H. Morsy, and I. Wegener. "Solution of the Knight's Hamiltonian Path Problem on Chessboards." Discrete Applied Math, volume 50, no.2, pp.125-134. 1994.
- ↑ Satyadev, Chaudhary. Kavyalankara of Rudrata (Sanskrit Text, with Hindi translation);. Delhi: Parimal Sanskrit Series No. 30.
പുറമെ നിന്നുള്ള കണ്ണികൾ[തിരുത്തുക]
- Richard W. Henderson, Eugene Roger Apodaca A Knight of Egodeth: Zen Raptured Quietude, 240 Solutions to the Knights Tour in form of Game Book
- Warnsdorff's Rule and its efficiency from Warnsdorff's Rule Web Page
- Mario Velucchi The ultimate Knight's Tour page of Links Archived 2004-08-06 at the Wayback Machine.
- The knight's tour Archived 2005-12-19 at the Wayback Machine.
- Knight's tour notes
- Sloane's Integer Sequence
 A001230
A001230 - Preprint of Pohl's paper (freely accessible)
- SilverKnight Archived 2011-10-06 at the Wayback Machine. - online knight's tour game
ഉത്തരങ്ങൾ[തിരുത്തുക]
- The Knight's Tour by Jay Warendorff, Wolfram Demonstrations Project
- A Simple backtracking implementation in C++ Archived 2013-11-14 at the Wayback Machine.
- An implementation in C# Archived 2017-09-26 at the Wayback Machine.
- Knight's Tours Using a Neural Network Program that creates tours using a neural network, plus gallery of images.
[[Category:ചെസ്സ്]
