വീറ്റ്സ്റ്റൺ ബ്രിഡ്ജ്

Wheatstone bridge circuit diagram. The unknown resistance R_x is to be measured; resistances R₁, R₂ and R₃ are known and R₂ is adjustable. If the measured voltage V_G is 0, then R₂/R₁ = R_x/R₃.

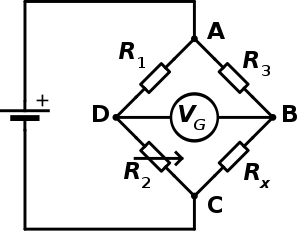
വീറ്റ്സ്റ്റൺ ബ്രിഡ്ജ് എന്നത് ഒരു ബ്രിഡ്ജ് സർക്ക്യൂട്ടിന്റെ രണ്ട് കാലുകൾ സന്തുലനം ചെയ്ത് അറിയാത്ത വൈദ്യുതപ്രതിരോധം കണ്ടുപിടിക്കാനായി ഉപയോഗിക്കുന്ന ഒരു വൈദ്യുത സർക്യൂട്ടാണ്. ഒരു കാലിൽ അറിയാത്ത ഘടകം ഉൾപ്പെടുന്നു. പ്രാഥമികമായും ഒരു വീറ്റ്സ്റ്റൺ ബ്രിഡ്ജിന്റെ ഗുണം എന്നത് ഏറ്റവും കൃത്യതയോടെ അളവുകൾ നൽകാനുള്ള അതിന്റെ കഴിവാണ്. യഥാർത്ഥ പൊട്ടൻഷ്യോമീറ്ററിന്റേതിനു സമാനമാണ് ഇതിന്റെ പ്രവർത്തനക്രമം.

1833ൽ സാമുവൽ ഹണ്ടർ ക്രിസ്റ്റിയാണ് വീറ്റ്സ്റ്റൺ ബ്രിഡ്ജ് കണ്ടെത്തിയത്. സർ ചാൾസ് വീറ്റ്സ്റ്റൺ 1843 ൽ ഇതിനെ മെച്ചപ്പെടുത്തി പ്രചരിപ്പിച്ചു. വീറ്റ്സ്റ്റൺ ബ്രിഡ്ജിന്റെ ആദ്യത്തെ ആവശ്യങ്ങളിൽ ഒന്ന് മണ്ണിന്റെ അപഗ്രഥനവും താരതമ്യവുമായിരുന്നു.

പ്രവർത്തനം

ചിത്രത്തിൽ, $\scriptstyle R_{x}$ എന്നത് അളക്കേണ്ട അറിയപ്പെടാത്ത പ്രതിരോധമാണ് ; $\scriptstyle R_{1},$ $\scriptstyle R_{2},$ , $\scriptstyle R_{3}$ എന്നിവ അറിയപ്പെടുന്ന പ്രതിരോധമുള്ള പ്രതിരോധകങ്ങളും പ്രതിരോധകം $\scriptstyle R_{2}$ ന്റെ പ്രതിരോധം ക്രമീക്കാവുന്നതുമാണ്. അറിയാവുന്ന കാലിലെ രണ്ട് പ്രതിരോധങ്ങളുടെ അംശബന്ധം $\scriptstyle (R_{2}/R_{1})$, അറിയപ്പെടാത്ത കാലിലെ പ്രതിരോധങ്ങൾക്കു $\scriptstyle (R_{x}/R_{3}),$ തുല്യമാണെങ്കിൽ രണ്ട് കേന്ദ്രബിന്ദുക്കൾ (B, D) തമ്മിലുള്ള പൊട്ടൻഷ്യൽ വ്യതിയാനം 0 ആയിരിക്കും. അപ്പോൾ ഗാൽവനോമീറ്റർ ലൂടെ കറന്റ് ഒഴുകുകയില്ല $\scriptstyle V_{g}.$. ബ്രിഡ്ജ് സന്തുലിതമല്ലെങ്കിൽ, വൈദ്യുതപ്രവാഹത്തിന്റെ ദിശ $\scriptstyle R_{2}$ വളരെ ഉയർന്നതാണോ, $\scriptstyle R_{2}$ വളരെ താഴ്ന്നതാണോ എന്ന് കാണിക്കുന്നു. ഗാല്വനോമീറ്ററിലൂടെ വൈദ്യുതപ്രവാഹം ഇല്ലാതാകുന്നതുവരെ വ്യത്യാസപ്പെട്ടുകൊണ്ടിരിക്കും. വൈദ്യുതപ്രവാഹം ഇല്ലാതാകുമ്പോൾ ഗാൽവനോമീറ്റർ റീഡിങ് 0 കാണിക്കും.

ഗാൽവനോമീറ്റർ ഉപയോഗിച്ച് സീറോകറന്റ് വളരെ കൃത്യമായി കണ്ടെത്താൻ കഴിയും. അതിനാൽ, $\scriptstyle R_{1},$ $\scriptstyle R_{2},$, $\scriptstyle R_{3}$എന്നിവ വളരെ കൃത്യമായി അറിയാം എങ്കിൽ $\scriptstyle R_{x}$ഉം വളരെ കൃത്യമായി അളക്കാൻ കഴിയും. $\scriptstyle R_{x}$ലെ വളരെ ചെറിയ മാറ്റങ്ങൾ പോലും സംന്തുലനത്തെ ബാധിക്കും. അവ അപ്പോൾത്തന്നെ കണ്ടെത്താനും കഴിയും.

സംതുലനബിന്ദുവിൽ, അംശബന്ധം:

${\begin{aligned}{\frac {R_{2}}{R_{1}}}&={\frac {R_{x}}{R_{3}}}\\[4pt]\Rightarrow R_{x}&={\frac {R_{2}}{R_{1}}}\cdot R_{3}\end{aligned}}$

മറ്റൊരു രീതിയിൽ, $\scriptstyle R_{1},$ $\scriptstyle R_{2},$ , $\scriptstyle R_{3}$ എന്നിവ അറിയാം, $\scriptstyle R_{2}$എന്നാൽ മാറ്റം വരുത്തുന്നില്ല എങ്കിൽ, കിർച്ചോഫിന്റെ സർക്യൂട്ട് നിയമങ്ങളുടെ സഹായത്താൽ $\scriptstyle R_{x},$ന്റെ മൂല്യം പൊട്ടൻഷ്യൽ വ്യതിയാനമോ അല്ലെങ്കിൽ മീറ്ററിലൂടെയുള്ള വൈദ്യുതപ്രവാഹമോ ഉപയോഗിച്ച് കണ്ടെത്താം.

നിർദ്ധാരണം

Directions of currents arbitrarily assigned

ആദ്യമായി, കിർച്ചോഫിന്റെ ആദ്യത്തെ നിയമമാണ് എന്നീ ജംഗ്ഷനുകളിലെ വൈദ്യുതപ്രവാഹങ്ങൾ കണ്ടെത്താനായി ഉപയോഗിക്കുന്നത്:

${\begin{aligned}I_{3}-I_{x}+I_{G}&=0\\I_{1}-I_{2}-I_{G}&=0\end{aligned}}$

എന്നിട്ട്, ABD, BCD എന്നീ ലൂപ്പുകളിലെ പൊട്ടൻഷ്യൽ കണ്ടെത്താനായി കിർച്ചോഫിന്റെ രണ്ടാം നിയമം ഉപയോഗിക്കുന്നു:

${\begin{aligned}(I_{3}\cdot R_{3})-(I_{G}\cdot R_{G})-(I_{1}\cdot R_{1})&=0\\(I_{x}\cdot R_{x})-(I_{2}\cdot R_{2})+(I_{G}\cdot R_{G})&=0\end{aligned}}$

ബ്രിഡ്ജ് സംതുലനത്തിലായിരിക്കുമ്പോൾ, I_G = 0 ആയിരിക്കും. അങ്ങനെ രണ്ടാമത്തെ കൂട്ടം സമവാക്യങ്ങളെ ഇങ്ങനെ മാറ്റിയെഴുതാം:

${\begin{aligned}I_{3}\cdot R_{3}&=I_{1}\cdot R_{1}\\I_{x}\cdot R_{x}&=I_{2}\cdot R_{2}\end{aligned}}$

എന്നിട്ട്, സമവാക്യങ്ങളെ ഹരിക്കുകയും ക്രമീകരിക്കുകയും ചെയ്യുമ്പോൾ ഇങ്ങനെ ലഭിക്കും:

$R_{x}={{R_{2}\cdot I_{2}\cdot I_{3}\cdot R_{3}} \over {R_{1}\cdot I_{1}\cdot I_{x}}}$

ആദ്യത്തെ നിയമത്തിൽ നിന്ന് I₃ = I_x, I₁ = I₂ എന്നും കാണാം. കണ്ടെത്തേണ്ട R_xന്റെ മൂല്യം താഴെത്തന്നിരിക്കുന്നതിൽ നിന്ന് ഇപ്പോൾ അറിയാം:

$R_{x}={{R_{3}\cdot R_{2}} \over {R_{1}}}$

ഇതും കാണുക

• Diode bridge, product mixer - diode bridges
• Phantom circuit – a circuit using a balanced bridge
• Post Office Box
• Potentiometer (measuring instrument)
• Potential divider
• Ohmmeter
• Resistance thermometer
• Strain gauge