യൂണിറ്റ് വൃത്തം

ആരം ഒരു യൂണിറ്റ് ഉള്ള വൃത്തത്തെയാണ് ഗണിതത്തിൽ യൂണിറ്റ് വൃത്തം എന്നു വിളിയ്ക്കുന്നത്. സാധാരണയായി യൂക്ളീഡിയൻ പ്രതലത്തിലെ (Euclidean Space) കാർത്തീയ നിർദ്ദേശാങ്കവ്യവസ്ഥയിൽ (Cartesian Coordinate System) ആധാരബിന്ദുവിനെ (0, 0) കേന്ദ്രമാക്കിയാണ് യൂണിറ്റ് വൃത്തം വരയ്ക്കുന്നത്.[1] സാധാരണ ഇതിനെ S1 എന്ന് അടയാളപ്പെടുത്താറുണ്ട്; ഉയർന്ന മാനത്തിലെ ഇതിന്റെ സാമാന്യവൽക്കരണം യൂണിറ്റ് ഗോളം എന്നാണ്. (x, y) എന്നത് ഈ വൃത്തത്തിന്റെ പരിധിയിലെ ഒരു ബിന്ദുവാണെങ്കിൽ, യഥാക്രമം |x| , |y| എന്നിവ 1 യൂണിറ്റ് കർണമുള്ള ഒരു മട്ടത്രികോണത്തിന്റെ പാദവും ലംബവുമാണ്. വൃത്തത്തിന്റെ കേന്ദ്രത്തിൽ നിന്നും ഈ ബിന്ദുവിലേയ്ക്ക് വരയ്ക്കുന്ന നേർരേഖയാണ് കർണം. ഈ കർണവും വൃത്തത്തിന്റെ ആരവും ഒന്നുതന്നെയാണ്. അതിനാലാണ് കർണത്തിന് 1 യൂണിറ്റ് നീളം വന്നത്. ഇനി ഈ ത്രികോണത്തിൽ പൈതഗോറസ് സിദ്ധാന്തം പ്രയോഗിച്ചാൽ താഴെക്കാണുന്ന സൂത്രവാക്യം കിട്ടും:
എല്ലാ x വിലകൾക്കും x2 = (−x)2 ആയതുകൊണ്ടും, ആദ്യ പാദംശത്തിലെ (quadrant) ഓരോ ബിന്ദുവിന്റേയും പ്രതിഫലനം യൂണിറ്റ് വൃത്തത്തിൽ തന്നെ വരുന്നതുകൊണ്ടും യൂണിറ്റ് വൃത്തത്തിലെ എല്ലാ പാദംശത്തിലെ ബിന്ദുക്കൾക്കും ഈ സൂത്രവാക്യം സാധുവായിരിയ്ക്കും.
കാർത്തീയ നിർദ്ദേശാങ്കവ്യവസ്ഥയ്ക്കു പുറമെ മറ്റുള്ള നിർദ്ദേശാങ്കവ്യവസ്ഥകളിലും യൂണിറ്റ് വൃത്തം വരയ്ക്കാവുന്നതാണ്. എന്നാൽ ഇത്തരം വ്യവസ്ഥകളിൽ ദൂരത്തിന്റെ നിർവചനം വ്യത്യസ്തമായതുകൊണ്ടു അതിൽ വരച്ചാൽ പുറത്തുകാണുന്ന ആകൃതി വൃത്താകാരം ആകണമെന്നില്ല. ഉദാഹരണത്തിന് ടാക്സികാബ് നിർദ്ദേശാങ്കവ്യവസ്ഥയിൽ ഇതൊരു സമചതുരം ആയിരിയ്ക്കും.[2]
സങ്കീർണപ്രതലത്തിലെ യൂണിറ്റ് വൃത്തം[തിരുത്തുക]
ആധാരബിന്ദുവിൽ നിന്നും ഒരു യൂണിറ്റ് അകലെയുള്ള സങ്കീർണസംഖ്യകളുടെ ഗണമാണ് സങ്കീർണപ്രതലത്തിലെ യൂണിറ്റ് വൃത്തം. അതായത് താഴെക്കാണുന്ന സൂത്രവാക്യം അനുസരിയ്ക്കുന്ന എല്ലാ സങ്കീർണസംഖ്യകളുടെയും ഗണം.
ഇതാണ് പ്രശസ്തമായ ഓയ്ലറുടെ സമവാക്യം.[3] ഇതിനെ ചുരുക്കി എന്നും എഴുതാം.[1]
യൂണിറ്റ് വൃത്തവും ത്രികോണമിതി ഫലനങ്ങളും[തിരുത്തുക]
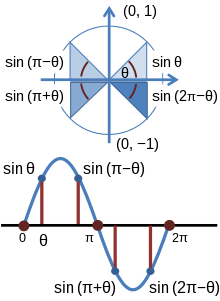
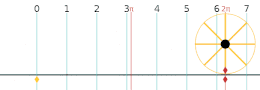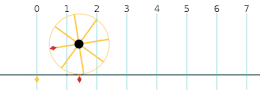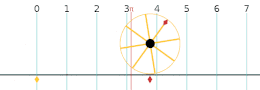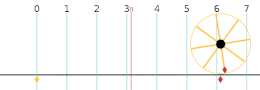
ത്രികോണമിതിയിലെ θ എന്ന കോണിന്റെ കോസൈൻ, സൈൻ ഫലനങ്ങൾ താഴെക്കാണുന്ന രീതിയിൽ ഒരു യൂണിറ്റ് വൃത്തത്തിൽ നിർണയിക്കാം: (x, y) എന്നത് യൂണിറ്റ് വൃത്തത്തിലെ ഒരു ബിന്ദുവാണെന്നും ആധാരബിന്ദുവിൽ നിന്നും ഈ ബിന്ദുവിലേക്കുള്ള ഒരു നേർരേഖ ധനാത്മക X നിർദ്ദേശാക്ഷവുമായി (positive X coordinate axis) കോൺ θ ഉണ്ടാക്കുന്നു എന്നും വിചാരിച്ചാൽ,
വൃത്തത്തിന്റെ x2 + y2 = 1 എന്ന സൂത്രവാക്യത്തിൽ നിന്നും താഴെക്കാണുന്ന ത്രികോണമിതി സമവാക്യം നേരിട്ട് കിട്ടും.
ത്രികോണമിതി ഫലനങ്ങൾ പഠിച്ചു തുടങ്ങുന്ന അവസ്ഥയിൽ സൈൻ, കോസൈൻ വിലകൾ സാധാരണയായി ഒരു മട്ടത്രികോണത്തിനുള്ളിലെ അംശബന്ധങ്ങൾ എന്ന നിലയിലാണ് പഠിയ്ക്കുന്നത്. ഈ അവസ്ഥയിൽ വ്യത്യസ്ത കോണുകളുടെ സൈൻ, കോസൈൻ വിലകൾ പഠിയ്ക്കുന്നുണ്ടെങ്കിലും ഈ കോണുകളുടെ വില ഒരിയ്ക്കലും 90 ഡിഗ്രിയിൽ കൂടാറില്ല (മട്ടത്രികോണത്തിലെ ഏറ്റവും വലിയ കോണിന്റെ അളവ് 90 ഡിഗ്രി ആണ്). യൂണിറ്റ് വൃത്തത്തിനെ അടിസ്ഥാനപ്പെടുത്തിയുള്ള ഈ ഫലനങ്ങളുടെ നിർവചനം 90 ഡിഗ്രിയിൽ കൂടിയ കോണളവുകളിൽ സൈൻ, കോസൈൻ വിലകൾ എങ്ങനെ പെരുമാറുന്നു എന്നത് കണ്ടുപിടിയ്ക്കൽ എളുപ്പമാക്കുന്നു. മുകളിലെ ചിത്രത്തിൽ നിന്നും കോണളവ് 90 ഡിഗ്രിയിൽ അല്പം കൂടുതൽ ആകുമ്പോൾ പരിധിയിലെ ബിന്ദു രണ്ടാമത്തെ പാദാംശത്തിൽ ആണെന്ന് കാണാം. ഇനി അതിന്റെ സൈൻ, കോസൈൻ വിലകൾ കിട്ടാൻ ആ ബിന്ദുവിന്റെ x, y നിർദ്ദേശാങ്കങ്ങൾ എടുത്താൽ മാത്രം മതി. ഇതേ പാത പിന്തുടർന്ന് 360 ഡിഗ്രി വരെയുള്ള കോണളവുകളുടെ സൈൻ, കോസൈൻ വിലകൾ കണ്ടു പിടിയ്ക്കാവുന്നതാണ്. 360 ഡിഗ്രി ആകുമ്പോഴേയ്ക്കും വൃത്തം ഒരു വട്ടം പൂർത്തിയാക്കും. പിന്നീടുള്ള കോണളവുകൾ 0 മുതൽ ഉള്ള അളവുകളുടെ ആവർത്തനം മാത്രമാണെന്ന് ചിത്രത്തിൽ നിന്നും വ്യക്തമാണല്ലോ. 720 ഡിഗ്രി വരെ ഇത് തുടരുകയും അതിനുശേഷം ഇത് വീണ്ടും 0 മുതൽ ആവർത്തിയ്ക്കുകയും ചെയ്യുന്നു. അതുപോലെ തന്നെ ന്യൂന അളവുകളിലുള്ള കോണുകളുടെ സൈൻ, കോസൈൻ വിലകൾ കാണാൻ ഇതേ ചിത്രം തന്നെ ഉപയോഗിയ്ക്കാം. അന്യൂന കോണളവുകൾ അന്യൂന X അക്ഷത്തിൽ നിന്നും അപ്രദക്ഷിണദിശയിലാണ് കൂടുന്നത്. അന്യൂന X അക്ഷത്തിൽ നിന്നും പ്രദക്ഷിണദിശയിൽ കോണുകൾ അളന്നാൽ ന്യൂനകോണളവുകൾ കിട്ടുന്നു. ഈ കോണുകളെ സൂചിപ്പിയ്ക്കുന്നു ബിന്ദുക്കളും യൂണിറ്റ് വൃത്തത്തിൽ തന്നെ കിടക്കുന്നതു കൊണ്ട് അവയുടെ X, Y നിർദ്ദേശാങ്കങ്ങൾ എടുത്താൽ കോസൈൻ, സൈൻ വിലകൾ കിട്ടും.
കോസൈൻ, സൈൻ ഫലനങ്ങളുടെ ഈ വ്യാഖ്യാനത്തിൽ നിന്നും ഈ ഫലനങ്ങൾ ആവർത്തിത ഫലനങ്ങൾ ആണെന്നു കാണാം.[4] കാരണം ഓരോ 360 ഡിഗ്രി കഴിയുമ്പോഴും (യൂണിറ്റ് വൃത്തത്തിൽ ഒരു വട്ടം ചുറ്റി വരുമ്പോഴും) കോസൈൻ, സൈൻ ഫലനങ്ങളുടെ വില വീണ്ടും പഴയതു പോലെ ആകുന്നുണ്ടല്ലോ. താഴെ കൊടുത്തിരിയ്ക്കുന്ന സൂത്രവാക്യം ഇക്കാര്യത്തെ കാണിയ്ക്കുന്നു.
ഇവിടെ k എന്ന നമ്പർ വൃത്തത്തിനു ചുറ്റും എത്ര വട്ടം ഇതുവരെ കറങ്ങി എന്നു സൂചിപ്പിയ്ക്കുന്നു. ആദ്യ കറക്കത്തിന് ഇതു 0 ആയിരിയ്ക്കും. തുടർന്ന് ഓരോ കറക്കത്തിനനുസരിച് 1, 2, 3 ... എന്നിങ്ങനെ കൂടുന്നു.
ഇവ കൂടി കാണുക[തിരുത്തുക]
അവലംബം[തിരുത്തുക]
- ↑ 1.0 1.1 "Unit Circle".
- ↑ "Taxicab Angles and Trigonometry". Department of Physics, Oregon State University. Archived from the original on 2018-04-17. Retrieved 27 ഏപ്രിൽ 2018.
- ↑ "Euler Formula".
- ↑ Markushevich, A. I. (1965). The Remarkable Sine Functions. Elsevier. p. 2. Retrieved 27 April 2019.








