ഉപഗ്രൂപ്പ്
ഒരു ഗ്രൂപ്പിന്റെ അശൂന്യ ഉപഗണം മാതൃഗ്രൂപ്പിന്റെ ദ്വയാങ്കസംക്രിയയുമായി ചേർത്തുനോക്കുമ്പോൾ ഗ്രൂപ്പുകളുടെ സ്വയംപ്രമാണസിദ്ധാന്തങ്ങൾ പാലിക്കുന്നുവെങ്കിൽ ആ ഉപഗണത്തെ ഗ്രൂപ്പിന്റെ ഉപഗ്രൂപ്പ് (subgroup) എന്ന് വിളിക്കുന്നു. അതായത്, ഒരു ഗ്രൂപ്പിന്റെ ഉപഗണം സ്വയം ഒരു ഗ്രൂപ്പാണെങ്കിൽ (ഇവിടെ സംക്രിയ മാതൃഗ്രൂപ്പിന്റെ തന്നെയാകണമെന്ന നിബന്ധനയുണ്ട്) ആ ഉപഗണം ഒരു ഉപഗ്രൂപ്പാണ്.
ഏതൊരു ഗ്രൂപ്പിനും തൽസമകം മാത്രമടങ്ങിയ ഗണം ഉപഗ്രൂപ്പായുണ്ട് - ഇതിനെ തുച്ഛ ഉപഗ്രൂപ്പ് എന്ന് വിളിക്കുന്നു. ഉപഗണം ഒരു ഉചിത ഉപഗണമാണെങ്കിൽ - അതായത്, മാതൃഗ്രൂപ്പിലെ ഒരംഗമെങ്കിലും ഉപഗ്രൂപ്പിൽ ഇല്ലാതുണ്ടെങ്കിൽ - ഉപഗ്രൂപ്പിനെ ഉചിത ഉപഗ്രൂപ്പ് എന്ന് വിളിക്കുന്നു
സവിശേഷതകൾ[തിരുത്തുക]
- ഉപഗ്രൂപ്പിലെ തൽസമകം മാതൃഗ്രൂപ്പിലെ തൽസമകം തന്നെയാണ്
- ഉപഗ്രൂപ്പിലെ ഓരോ അംഗത്തിന്റെയും വിപരിത അംഗം മാതൃഗ്രൂപ്പിലെ വിപരിത അംഗം തന്നെയാണ്
- രണ്ട് ഉപഗ്രൂപ്പുകളുടെ സംഗമവും ഒരു ഉപഗ്രൂപ്പാണ്
- രണ്ട് ഉപഗ്രൂപ്പുകളുടെ യോഗം ഒരു ഉപഗ്രൂപ്പാവണമെങ്കിൽ ഒന്ന് മറ്റൊന്നിന്റെ ഉപഗണമായിരിക്കണം
- ഉപഗ്രൂപ്പിന്റെ കോടി മാതൃഗ്രൂപ്പിന്റെ കോടിയുടെ ഘടകമായിരിക്കും. മാതൃഗ്രൂപ്പിന്റെ കോടിയെ ഉപഗ്രൂപ്പിന്റെ കോടി കൊണ്ട് ഹരിച്ചാൽ കിട്ടുന്ന സംഖ്യയെ സൂചകാങ്കം എന്ന് വിളിക്കുന്നു. ഉപഗ്രൂപ്പിന്റെ സഹഗണങ്ങളുടെ എണ്ണമാണിത്
ഉദാഹരണം[തിരുത്തുക]
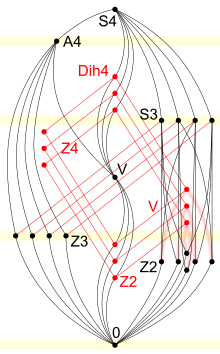
സമമിതീയഗ്രൂപ്പായ S4 ന്റെ ഉപഗ്രൂപ്പുകൾ ഇവയാണ്:
- തുച്ഛ ഉപഗ്രൂപ്പ് { e }
- ചാക്രികഗ്രൂപ്പായ Z2 ന് സമരൂപമായ 9 ഉപഗ്രൂപ്പുകൾ
- ചാക്രികഗ്രൂപ്പായ Z3 ന് സമരൂപമായ 4 ഉപഗ്രൂപ്പുകൾ
- ചാക്രികഗ്രൂപ്പായ Z4 ന് സമരൂപമായ 3 ഉപഗ്രൂപ്പുകൾ
- ക്ലൈൻ ഗ്രൂപ്പിന് സമരൂപമായ 4 ഉപഗ്രൂപ്പുകൾ
- സമമിതീയഗ്രൂപ്പായ S3 ന് സമരൂപമായ 4 ഉപഗ്രൂപ്പുകൾ
- ഡൈഹെഡ്രൽ ഗ്രൂപ്പായ D4 ന് സമരൂപമായ 3 ഉപഗ്രൂപ്പുകൾ
- പ്രത്യാവർത്തിഗ്രൂപ്പായ A4
- മാതൃഗ്രൂപ്പായ S4 തന്നെ
