പരവലയം

ഇംഗ്ലീഷ് വിലാസം

https://ml.wikipedia.org/wiki/Parabola

ഒരു പരാബൊള

പ്രതിഫലത,നിയതരേഖ(പച്ച), നിയതരേഖയേയും ഫോകസിനേയും ബന്ധിപ്പിക്കുന്ന വരകൾ(നീല) എന്നിവ കാണിക്കുന്ന ഒരു ആരേഖം

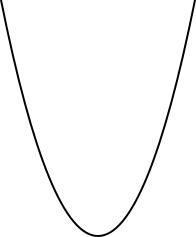
ദ്വിമാനതലത്തിൽ രചിച്ചിരിക്കുന്ന ഒരുതരം വക്രമാണ് പരാബൊള. ഒരു സമതലത്തിൽ ശയിക്കുന്ന ഒരു രേഖയും , ആ രേഖയിലല്ലാത്ത ഒരു ബിന്ദുവും ഉണ്ടെന്നിരിക്കട്ടെ; ആ രേഖയിൽ നിന്നും (നിയതരേഖ; Directrix) ബിന്ദുവിൽ നിന്നും ( കേന്ദ്രം; focus) ഉള്ള അകലം തുല്യമാകത്തക്കവിധം സഞ്ചരിക്കുന്ന മറ്റൊരു ബിന്ദുവിന്റെ സഞ്ചാരപഥത്തെ ( Locus) ആണ് പരാബൊള (Parabola) എന്നു പറയുന്നത്.

ഒരു നേർവൃത്തസ്തൂപികയെ അതിന്റെ ഏതെങ്കിലും ഒരു പാർശ്വരേഖയ്ക് സമാന്തരമായി ഒരു സമതലം ഛേദിക്കുമ്പോൾ ലഭിക്കുന്ന ദ്വിമാനവക്രരൂപവും പരാബോളയാണ്. വൃത്തസ്തൂപികയുടെ ശീർഷവും (Vertex) അതിന്റ ആധാരവൃത്തത്തിലെ ഏതെങ്കിലും ഒരു ബിന്ദുവും ബന്ധിപ്പിക്കുന്ന ഋജുരേഖയെയാണ് പാർശ്വരേഖ എന്നു പറയുന്നത്. വൃത്തസ്തൂപികയെ ഛേദിക്കുന്ന തലത്തിന്, അതിന്റെ അക്ഷവുമായുണ്ടാകുന്ന ചരിവ് അനുസരിച്ച്, പല ദ്വിമാനവക്രങ്ങൾ ലഭിക്കുന്നു. വൃത്തം, ദീർഘവൃത്തം, പരാബൊള, ഹൈപ്പർബൊള എന്നിവയാണവ. എന്നാൽ, ഛേദതലം, പ്രസ്തുത നേർവൃത്തസ്തൂപികയെ ഛേദിക്കാതെ അതിന്റെ വക്രപ്രതലം സ്പർശിക്കുക മാത്രം ചെയ്യുമ്പോൾ, ഒരു ഋജുരേഖയാണ് ലഭിക്കുന്നത്. ഇങ്ങനെ നേർവൃത്തസ്തൂപിക ഛേദിച്ചാൽ കിട്ടുന്ന വക്രങ്ങളെ പൊതുവെ വൃത്തസ്തുപികാവക്രങ്ങൾ (Conics) എന്നു പറയുന്നു.

ഭൗതികശാസ്ത്രത്തിലും ജ്യോതിശാസ്ത്രത്തിലും സാങ്കേതികവിദ്യാരംഗങ്ങളിലും, മറ്റനവധി ശാസ്ത്രമേഖലകളിലും പരാബൊളക്ക് വളരെ പ്രാധാന്യമുണ്ട്.

ഒരു ഗോളത്തിന്റെ ഗുരുത്വാകർഷണത്തിനു വിധേയമായി, ക്ഷേപിക്കപ്പെടുന്ന ഒരു വസ്തുവിന്റെ (എറിയപ്പെടുന്ന ഒരു ക്രിക്കറ്റുപന്ത്, തോക്കിൽ നിന്നു പായുന്ന ഒരു വെടിയുണ്ട മുതലായവ) സഞ്ചാരപഥം പരാബോളയാണ്.

വിശ്ലേഷണജ്യാമിതീസമവാക്യങ്ങൾ

ചതുരനിർദ്ദേശാങ്കവ്യവസ്ഥയിൽ $y\,\!$ അക്ഷത്തിനു സമാന്തരമായതും ശീർഷം $(h,k)\,\!$ഉം ഫോകസ് $(h,k+p)\,\!$ഉം നിയതരേഖ $y=k-p\,\!$ഉം $p\,\!$ ദൂരവും ഉള്ള പരാബോളയുടെ സമവാക്യം

$(x-h)^{2}=4p(y-k)\,$ ആണ്.

മറ്റൊരു തരത്തിൽ x-അക്ഷത്തിനു സമാന്തരമായ പരാബോളയുടെ സമവാക്യം

$(y-k)^{2}=4p(x-h)\,$ ഇപ്രകാരമാണ്‌

പൊതുസമവാക്യം

$Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0\,$ ഇപ്രകാരമാണ്.

ഇതര ജ്യാമിതീയ നിർ‌വചനങ്ങൾ

നാലുതരം വൃത്തസ്തുപികാവക്രങ്ങൾ

വൃത്തസ്തുപികാവക്രങ്ങളിൽ, ഏതു ബിന്ദുവിൽ നിന്നും, കേന്ദ്രത്തിലേക്കും, നിയതരേഖയിലേക്കും ഉള്ള ദൂരങ്ങൾ തമ്മിലുള്ള അനുപാതത്തെ വക്രത്തിന്റെ ഉത്കേന്ദ്രത (Eccentricity) എന്നു വിളിക്കുന്നു. അതായത്, വക്രത്തിലെ ഒരു ബിന്ദുവിൽ നിന്നും കേന്ദ്രത്തിലേക്കുള്ള അകലം r എന്നും, അതിൽ നിന്നും നിയതരേഖയിലേക്കുള്ള അകലം s എന്നുമിരിക്കട്ടെ, എങ്കിൽ -

ഉത്കേന്ദ്രത, $e={\frac {r}{s}}\,$

പരാബൊളയുടെ കാര്യത്തിൽ, മേൽപ്പറഞ്ഞ അകലങ്ങൾ തുല്യമായതിനാൽ, ഉത്‌കേന്ദ്രത ഒന്ന് ആയിരിക്കും. ഉത്കേന്ദ്രത ഒന്നിൽക്കുറവാണെങ്കിൽ അതു ദീർഘവൃത്തവും (ellipse) , ഒന്നിൽ കൂടുതലാണെങ്കിൽ അത് ഹൈപ്പർബൊളയും ആയിരിക്കും. ഉത്കേന്ദ്രത പൂജ്യം ആയ വക്രമാണ് വൃത്തം.

ദീർഘവൃത്തങ്ങളുടെ ശ്രേണിയുടെ സീമ എന്ന നിലയിൽ പരാബോളയെ പരിഗണിക്കാം.ഈ ദീർഘവൃത്തങ്ങളുടെ ഒരു ഫോകസ് ഉറപ്പിച്ചും അടുത്ത ഫോകസ് ഒരേ ദിശയിൽ തന്നെ അനിയന്ത്രിതമായി നീങ്ങാനും അനുവദിക്കുന്നു.ഇത്തരത്തിൽ പരാബോളയെ ഒരു ഫോകസ് അനന്തതയിൽ കേന്ദ്രീകരിച്ചിരിക്കുന്ന ഒരു ദീർഘവൃത്തമായി പരിഗണിക്കാം.

പരബോളക്ക് പ്രതിഫലന പ്രതിസമതയുള്ള ഒരു അക്ഷം ഉണ്ട്. ഈ അക്ഷം പരാബോളയുടെ ഫോകസിലൂടെ കടന്നുപോകുന്നു.നിയതരേഖക്ക് ഇത് ലംബവും ആണ്. ഈ അക്ഷത്തിന്റേയും പരാബോളയുടേയും സംഗമബിന്ദുവാണ് പരാബോളയുടെ ശീർഷം.

സമവാക്യങ്ങൾ

ശീർഷം (h, k)ഉം ഫോകസും ശീർഷവും തമ്മിലുള്ള ദൂരം pഉം ആയ പരാബോളയുടെ സമവാക്യങ്ങളാണ് താഴേ പ്രസ്താവിക്കുന്നത്.

കാർടീഷ്യൻ

ലംബഅക്ഷത്തിലുള്ള പ്രതിസമത

$(x-h)^{2}=4p(y-k)\,$

$y=k\,$

$y=ax^{2}+bx+c\,$

${\mbox{where }}a={\frac {1}{4p}};\ \ b={\frac {-h}{2p}};\ \ c={\frac {h^{2}}{4p}}+k;\ \$

$h={\frac {-b}{2a}};\ \ k={\frac {4ac-b^{2}}{4a}}$.

$x(t)=2pt+h;\ \ y(t)=pt^{2}+k\,$

തിരശ്ചീന അക്ഷത്തിലുള്ള പ്രതിസമത

$(y-k)^{2}=4p(x-h)\,$

$x=a(y-k)^{2}+h\,$

$x=ay^{2}+by+c\,$

${\mbox{where }}a={\frac {1}{4p}};\ \ b={\frac {-k}{2p}};\ \ c={\frac {k^{2}}{4p}}+h;\ \$

$h={\frac {4ac-b^{2}}{4a}};\ \ k={\frac {-b}{2a}}$.

$x(t)=pt^{2}+h;\ \ y(t)=2pt+k\,$

പൊതുവായ പരാബോള

പരാബോളയുടെ പൊതുരൂപം

$(Ax+By)^{2}+Cx+Dy+E=0\,$ ആണ്

കോണികത്തിന്റെ പൊതുസമവാക്യത്തിൽ നിന്നും നിർ‌വചിച്ചിരിക്കുന്ന പരാബോളയുടെ സമവാക്യം $B^{2}=4AC$ ആണ്‌.

നാഭിലംബം,അർദ്ധനാഭിലംബം,ധ്രുവീയ നിർദ്ദേശാങ്കങ്ങൾ

ധ്രുവീയ നിർദ്ദേശാങ്കത്തിൽ(polar co-ordinates) ഫോകസ് മൂലബിന്ദുവും നിയതരേഖ അക്ഷത്തിനു സമാന്തരവും ആയ പരാബോളയുടെ സമവാക്യം

$r(1+\cos \theta )=l\,$ ആണ്.

l അർദ്ധനാഭികേന്ദ്രം(semi-latus rectum) ,അതായത് ഫോകസിൽ നിന്നും പരാബോളയിലേക്കുള്ള ദൂരം ആണ്.നാഭികേന്ദ്രം(latus rectum) ഫോകസിലൂടെ കടന്നുപോകുന്ന അക്ഷത്തിനു ലംബമായ ഞാൺ ആണ്.ഇതിന്റെ നീളം 4l ആണ്‌.

ഫോകസിന്റെ അനുമാനം

നിയതരേഖ(L),ഫോകസ്(F) എന്നിവ കാണിക്കുന്ന ഒരു പരാബോളിക് വക്രം.തന്നിരിക്കുന്ന ഒരു ബിന്ദു P_nൽ നിന്നും ഫോകസിലേക്കുള്ള ദൂരം P_n ൽ നിന്നും നിയതരേഖയിലുള്ള Q_nലേക്കുള്ള ദൂരത്തിനു തുല്യമാണ്.

ഒരു രേഖ(L),ഫോകസ്(F),ശീർഷം(V) എന്നിവ ചിത്രീകരിക്കുന്ന പരാബോളിക് വക്രം . പ്രതിസമതാ അക്ഷത്തിനു ലംബവും ശീർഷത്തിൽ നിന്നും പരാബോളയുടെ ഫോകസിന് വിപരീതവും ആയ നിയമബന്ധിതമല്ലാത്ത ഒരു രേഖയാണ് L.ഏതൊരു രേഖയുടേയും നീളം F - P_n - Q_n തുല്യമായിരിക്കും.ഇതുവഴി ഒരു ഫോകസ് അനന്തത്തിലായ ഒരു ദീർഘവൃത്തമാണ് പരാബോള എന്ന് പറയാം.

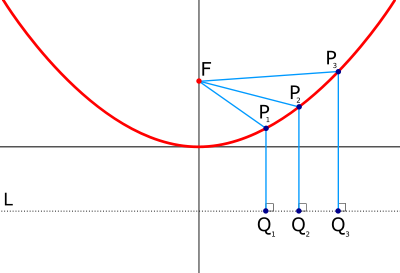
പ്രതിസമത അക്ഷം y-അക്ഷത്തിനു സമാന്തരമായതും ശീർഷം (0,0) ആയതും ആയ ഒരു പരാബോളയുടെ സമവാക്യം

$y=ax^{2},\qquad \qquad \qquad (1)$

ആണ്.(0,f)എന്ന ബിന്ദു പരാബോളയുടെ ഫോകസ് ആണ്.പരാബോളയിലുള്ള ഏതൊരു ബിന്ദുവും ഫോകസിൽ നിന്നും പ്രതിസമതാ അക്ഷത്തിനു ലംബമായ ഒരു രേഖയിൽ നിന്നും(ലീനിയാ നിയതരേഖ)തുല്യ അകലത്തിലായിരിക്കും.ശീർഷം ഇത്തരത്തിലുള്ള ഒരു ബിന്ദുവായതിനാൽ ലീനിയ നിയതരേഖ എന്ന ബിന്ദുവിലൂടേയും കടന്നുപോകുന്നു.അതായത് ഏതൊരു ബിന്ദു P=(x,y)ഉം (0,f)ൽ നിന്നും (x,-f)ൽ നിന്നും തുല്യ അകലത്തിലായിരിക്കും.ഇത്തരമൊരു സവിശേഷതയുള്ള ഫോകസിന്റെ വിലയാണ് കണ്ടുപിടിക്കുന്നത്.

Fഎന്നത് ഫോകസിനേയും Q,(x,-f)എന്ന ബിന്ദുവിനേയും സൂചിപ്പിക്കുന്നു. FP,QP എന്നിവയുടെ നീളം തുല്യമാണ്.

$\|FP\|={\sqrt {x^{2}+(y-f)^{2}}},$

$\|QP\|=y+f.$

$\|FP\|=\|QP\|$

${\sqrt {x^{2}+(ax^{2}-f)^{2}}}=ax^{2}+f\qquad$

ഇരുവശത്തിന്റേയും വർഗ്ഗം കണ്ടാൽ

$x^{2}+a^{2}x^{4}+f^{2}-2ax^{2}f=a^{2}x^{4}+f^{2}+2ax^{2}f\quad$

ഇരുവശത്തേയും പദങ്ങളെ വെട്ടിക്കളഞ്ഞാൽ

$x^{2}-2ax^{2}f=2ax^{2}f,\quad$

$x^{2}=4ax^{2}f.\quad$

ഇരുവശത്തുനിന്നും x വെട്ടിക്കളഞ്ഞാൽ( xപൂജ്യമാവില്ല)

$1=4af\quad$

$f={1 \over 4a}$

p=f എന്ന് കരുതിയാൽ പരാബോളയുടെ സമവാക്യം

$x^{2}=4py\quad$ എന്ന് കിട്ടുന്നു.

മൂലബിന്ദു കേന്ദ്രമായ ഒരു പരാബോളയുടെ സമവാക്യമാണ് മുകളിൽ പ്രതിപാദിച്ചിരിക്കുന്നത്.പരാബോളയുടെ പൊതുരൂപം :$y=ax^{2}+bx+c$ ആണ്.ഈ പരാബോളയുടെ ഫോകസ്

$\left({\frac {-b}{2a}},{\frac {-b^{2}}{4a}}+c+{\frac {1}{4a}}\right)$ ആണ്‌.

ഇതിനെ മറ്റൊരു രീതിയിൽ

$\left({\frac {-b}{2a}},c-{\frac {b^{2}-1}{4a}}\right)$ ഇങ്ങനേയും എഴുതാം

നിയതരേഖയെ

$y={\frac {-b^{2}}{4a}}+c-{\frac {1}{4a}}$

എന്ന സമവാക്യം കൊണ്ടും സൂചിപ്പിക്കം.ഈ സമവാക്യത്തെ തന്നെ മറ്റൊരു രീതിയിൽ

$y=c-{\frac {b^{2}+1}{4a}}$ ഇങ്ങനേയും എഴുതാം.

സ്പർശകത്തിന്റെ പ്രതിഫലനസ്വഭാവം

പരാബോളയുടെ സ്പർശകത്തിന്റെ ചെരിവ് ആണ്.ഈ രേഖ y-അക്ഷത്തിൽ (0,-y) = (0, - a x²) എന്ന ബിന്ദുവിലും x-അക്ഷത്തിൽ (x/2,0) എന്ന ബിന്ദുവിലും സംഗമിക്കുന്നു.ഈ ബിന്ദുവിനെ G എന്ന് വിളിക്കുന്നു.Gഎന്ന ബിന്ദു F ന്റേയുംQന്റേയും മദ്ധ്യബിന്ദു ആണ്.

${dy \over dx}=2ax={2y \over x}$:$F=(0,f),\quad$

$Q=(x,-f),\quad$

${F+Q \over 2}={(0,f)+(x,-f) \over 2}={(x,0) \over 2}=({x \over 2},0).$

G,FQന്റെ മദ്ധ്യബിന്ദു ആണെന്നതിനാൽ

$\|FG\|\cong \|GQ\|,$

കൂടാതെ P, Fൽ നിന്നും Qൽ നിന്നും തുല്യ അകലത്തിലാണ്.

$\|PF\|\cong \|PQ\|,$

മൂന്നാമതായി GP എന്ന രേഖ അതിനോടുതന്നെ സമമായതിനാൽ

$\Delta FGP\cong \Delta QGP$

ഇതിൽനിന്നും $\angle FPG\cong \angle GPQ$. എന്ന്കിട്ടുന്നു.QP എന്ന രേഖയെ P യിൽ നിന്നും Tഎന്ന ബിന്ദുവിലേക്കും GPഎന്ന രേഖയെ P ൽ നിന്നുംRഎന്ന ബിന്ദുവിലേക്കും നീട്ടിവരക്കാൻ സാധിക്കും.അപ്പോൾ $\angle RPT$ and $\angle GPQ$ ലംബങ്ങളായിരിക്കും.ആയതിനാൽ ഇവ സർവസമങ്ങളും ആയിരിക്കും.എന്നാൽ $\angle GPQ$ ,$\angle FPG$സമങ്ങളായതിനാൽ $\angle RPT$ , $\angle FPG$ഇവയും സമങ്ങളായിരിക്കും.പരാബോളയിലെ Pഎന്ന ബിന്ദുവിലെ സ്പർശകമാണ് RG എന്ന രേഖ.

അവലംബം

Encarta Reference Library Premium 2005