ബബിൾ സോർട്ട്

ഇംഗ്ലീഷ് വിലാസം

http://ml.wikipedia.org/wiki/Bubble_sort

ബബിൾ സോർട്ട്

സംഖ്യകളുടെ ഒരു ലിസ്റ്റിൽ ബബിൾ സോർട്ട് നടക്കുമ്പോൾ സംഭവിക്കുന്നത്.
കുടുംബം	സോർട്ടിങ്ങ് അൽഗൊരിതം
ഡാറ്റാ സ്ട്രക്‌ചർ	അറേ
മോശം സമയസങ്കീർണ്ണത	$O(N^2)$
നല്ല സമയസങ്കീർണ്ണത	$O(N)$
ശരാശരി സമയസങ്കീർണ്ണത	$O(N^2)$
മോശം മെമ്മറി സങ്കീർണ്ണത	ആകെ $O(N)$, ലിസ്റ്റിനു പുറമെ $O(1)$
Optimal	അല്ല

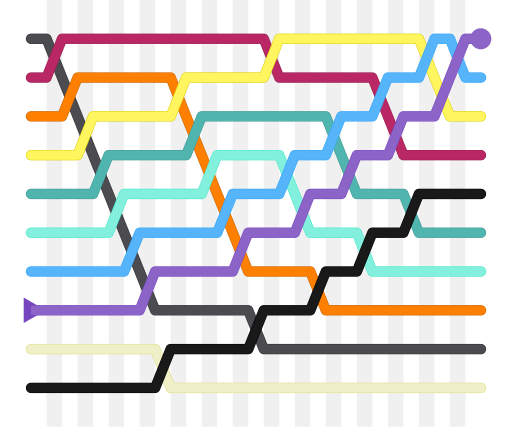
ഒരു ലിസ്റ്റിലെ സംഖ്യകളെയും മറ്റും ക്രമത്തിലാക്കാൻ ഉപയോഗിക്കുന്ന ഒരു സോർട്ടിങ്ങ് അൽഗൊരിതമാണ്‌ ബബിൾ സോർട്ട്. എളുപ്പമുള്ളതും, എന്നാൽ ഗണനപരമായ സങ്കീർണ്ണത കൂടിയതിനാൽ വളരെ സമയമെടുക്കുന്നതുമായ ഒരു സോർട്ടിങ്ങ് അൽഗൊരിതമാണിത്. ഇതിന്റെ സമയസങ്കീർണ്ണത $O(N^2)$ ഉം മെമ്മറി സങ്കീർണ്ണത $O(N)$ ഉമാണ്‌. എന്നാൽ ഒരു in-place അൽഗൊരിതമാണ്‌ ഇത് എന്നതിനാൽ ലിസ്റ്റിന്‌ പുറമെ O(1) മെമ്മറി മാത്രമേ ഇതിന്‌ ആവശ്യമുള്ളൂ.

ക്രമത്തിലല്ലാതെയുള്ള അടുത്തടുത്തുള്ള സംഖ്യകളെ പരസ്പരം മാറ്റുന്നതു വഴിയാണ്‌ ബബിൾ സോർട്ട് സംഖ്യകളെ ക്രമീകരിക്കുന്നത്. ക്രമീകരിക്കപ്പെട്ട സംഖ്യകൾ കുമിളകളെപ്പോലെ ലിസ്റ്റിന്റെ ഒരു ഭാഗത്തേക്കു പോകുന്നു എന്നതിനാലാണ്‌ ഈ അൽഗൊരിതത്തിന്‌ പേര്‌ ലഭിച്ചത്. സംഖ്യകളെ താരതമ്യം ചെയ്യുക വഴിയാണ്‌ സോർട്ടിങ്ങ് നടത്തുന്നത് എന്നതിനാൽ ഇത് ഒരു താരതമ്യ സോർട്ട് ആണ്‌.

അൽഗൊരിതം

(1,2) മുതൽ (N-1,N) വരെയുള്ള സംഖ്യാദ്വയങ്ങളെ പരിഗണിക്കുക. ഒരു ദ്വയം ക്രമത്തിലല്ലെങ്കിൽ ആ രണ്ട് സംഖ്യകളെ പരസ്പരം മാറ്റുക. ഇങ്ങനെ ചെയ്യുന്നതു വഴി ഏറ്റവും വലിയ സംഖ്യ ലിസ്റ്റിന്റെ ഏറ്റവും അവസാനമായി മാറും. ഇതിനുശേഷം ഈ പ്രക്രിയ ലിസ്റ്റിലെ ആദ്യത്തെ N-1, N-2....2 സംഖ്യകൾക്ക് തുടർന്നാൽ ലിസ്റ്റിലെ സംഖ്യകളെല്ലാം ക്രമത്തിലാകും

സ്യൂഡോകോഡ്

N സംഖ്യകളുള്ള array എന്ന ലിസ്റ്റ് ബബിൾ സോർട്ട് വഴി ക്രമത്തിലാക്കാൻ:

1. end <- N
2. flag <- ശരി
3. end = 1 അഥവാ flag = തെറ്റ് ആണെങ്കിൽ നിർത്തുക
4. flag <- തെറ്റ്
5. i <- 1 മുതൽ end-1 വരെ വിലകളുപയോഗിച്ച് പടി 6 ചെയ്യുക
6. array[i] array[i+1] നെക്കാൾ വലുതാണെങ്കിൽ അവയെ പരസ്പരം മാറ്റുകയും flag <- ശരി ആക്കുകയും ചെയ്യുക
7. end <- end - 1
8. പടി 3 ലേക്ക് പോകുക

ഇതും കാണുക

വിവരസാങ്കേതികവിദ്യ കവാടം

വിശകലനം

സംഖ്യകൾ തികച്ചും വിപരീതക്രമത്തിലാകുമ്പോൾ $\frac{N\left(N-1\right)}{2}$ തവണ പടി 6 ചെയ്യേണ്ടി വരുന്നു എന്നതിനാൽ ബബിൾ സോർട്ടിന്റെ മോശം സമയസങ്കീർണ്ണത $O(N^2)$ ആണ്‌. സംഖ്യകൾ തികച്ചും ക്രമത്തിലാകുമ്പോൾ ഇത് $N-1$ തവണ മാത്രം ചെയ്താൽ മതി. അതിനാൽ നല്ല സമയസങ്കീർണ്ണത $O(N)$ ആണ്‌. ശരാശരി സമയസങ്കീർണ്ണത $O(N^2)$ തന്നെ. ശരാശരി, മോശം സമയസങ്കീർണ്ണതകൾ $O(N \log N)$ ആയുള്ള സോർട്ടിങ്ങ് അൽഗൊരിതങ്ങൾ ഉണ്ട്. $O(N^2)$ സമയസങ്കീർണ്ണത ഉള്ള ഇൻസർഷൻ സോർട്ട് മുതലായ അൽഗൊരിതങ്ങളും ബബിൾ സോർട്ടിനെക്കാൾ വേഗത്തിൽ സോർട്ടിങ്ങ് നടത്തുന്നു എന്നതിനാൽ വലിയ ലിസ്റ്റുകൾ സോർട്ട് ചെയ്യാൻ ബബിൾ സോർട്ട് ഉപയോഗിക്കാറില്ല.

പുറത്തേക്കുള്ള കണ്ണികൾ

വിക്കിമീഡിയ വിക്കിപാഠശാലയിൽ ഈ ലേഖനവുമായി ബന്ധപ്പെട്ട

പരിശീലനക്കുറിപ്പുകൾ Algorithm implementation എന്ന താളിൽ ലഭ്യമാണ്

• Bubble Sort in 29 languages
• Animated Sorting Algorithms: Bubble Sort – graphical demonstration and discussion of bubble sort
• Bubble Sort Demo
• Bubble Sort Demonstration
• Lafore's Bubble Sort
• Sorting Applets in C++
• Analyze Bubble Sort in an online Javascript IDE
• A colored graphical Java applet which allows experimentation with initial state and shows statistics
• BubbleSort tutorial, code, and a simple example
• An animated video that explains bubble sort and quick sort and compares their performance.
• A much better visualization of the action of bubble sort.