"വ്യാസം" എന്ന താളിന്റെ പതിപ്പുകൾ തമ്മിലുള്ള വ്യത്യാസം
No edit summary |
|||
| വരി 23: | വരി 23: | ||
== സാമാന്യവത്കരണം == |
== സാമാന്യവത്കരണം == |
||
മേൽപറഞ്ഞ നിർവചനങ്ങൾ വൃത്തം, ഗോളം, [[ഉത്തലം]](convex) ആയ [[ദ്വിമാനം|ദ്വിമാന]]രൂപങ്ങൾ എന്നിവക്കു മാത്രം ബാധകമായതാണ്. |
മേൽപറഞ്ഞ നിർവചനങ്ങൾ വൃത്തം, ഗോളം, [[ഉത്തലം]](convex) ആയ [[ദ്വിമാനം|ദ്വിമാന]]രൂപങ്ങൾ എന്നിവക്കു മാത്രം ബാധകമായതാണ്. എന്നാൽ, [[ഹൈപ്പർ ക്യൂബ്]] പോലുള്ള, ഉത്തലമോ അപതലമോ ആയ, N-മാനങ്ങളുള്ള ജ്യാമിതീയ രൂപങ്ങൾക്കും, |
||
’ഒരുകൂട്ടം ചിതറിക്കിടക്കുന്ന ബിന്ദുക്കൾക്കും’ ബാധകമായ പൊതുവായ സാമാന്യവത്കൃത നിർവചനവും ഉണ്ട് |
|||
The definitions given above are only valid for circles, spheres and convex shapes. However, they are special cases of a more general definition which is valid for any kind of ''n''-dimensional convex or non-convex object, such as a [[hypercube]] or a set of scattered points. The '''diameter''' of a [[subset]] of a [[metric space]] is the [[supremum|least upper bound]] of the distances between pairs of points in the subset. So, if ''A'' is the subset, the diameter is |
|||
ഒരു [[മെട്രിക് സ്പെയ്സിലെ]] [[ഉപഗണം||ഉപഗണത്തിന്റെ]] '''വ്യാസം''', ഉപഗണത്തിലെ ബിന്ദു-ജോടികൾ തമ്മിലുള്ള ദൂരത്തിന്റെ [[ലീസ്റ്റ് അപ്പർ ബൗണ്ട്]] ആയിരിക്കും. അതായത് ''ആ'' ഒരു [[ഉപഗണം]] ആണെങ്കിൽ വ്യാസം |
|||
:[[supremum|sup]] { d(''x'', ''y'') | ''x'', ''y'' ∈ ''A'' } . |
:[[supremum|sup]] { d(''x'', ''y'') | ''x'', ''y'' ∈ ''A'' } . |
||
If the [[distance function]] d is viewed here as having [[codomain]] '''R''' (the set of all [[real number]]s), this implies that the diameter of the [[empty set]] (the case {{nowrap|1=''A'' = ∅}}) equals −∞ ([[negative infinity]]). Some authors prefer to treat the empty set as a special case, assigning it a diameter equal to 0,<ref>[http://at.yorku.ca/cgi-bin/bbqa?forum=ask_a_topologist_2004;task=show_msg;msg=0860.0002 Re: diameter of an empty set]</ref> which corresponds to taking the codomain of d to be the set of nonnegative reals. |
If the [[distance function]] d is viewed here as having [[codomain]] '''R''' (the set of all [[real number]]s), this implies that the diameter of the [[empty set]] (the case {{nowrap|1=''A'' = ∅}}) equals −∞ ([[negative infinity]]). Some authors prefer to treat the empty set as a special case, assigning it a diameter equal to 0,<ref>[http://at.yorku.ca/cgi-bin/bbqa?forum=ask_a_topologist_2004;task=show_msg;msg=0860.0002 Re: diameter of an empty set]</ref> which corresponds to taking the codomain of d to be the set of nonnegative reals. |
||
12:55, 7 മേയ് 2013-നു നിലവിലുണ്ടായിരുന്ന രൂപം

ജ്യാമിതിയിൽ, വൃത്തപരിധിലെ രണ്ട് ബിന്ദുക്കളെ തമ്മിൽ യോജിപ്പിച്ചു കൊണ്ട് വൃത്തത്തിന്റെ കേന്ദ്രത്തിൽ കൂടി കടന്നു പോകുന്ന രേഖാഖണ്ഡത്തെ ആ വൃത്തത്തിന്റെ വ്യാസം എന്നു പറയുന്നു. വ്യാസത്തെ, ഒരു വൃത്തത്തിന്റെ ഏറ്റവും നീളം കൂടിയ ഞാൺ എന്നും നിർവചിക്കാവുന്നതാണ്.
മേൽപറഞ്ഞ രണ്ട് നിർവചനങ്ങളും വൃത്തത്തിനു പുറമേ, ഗോളത്തിനും ബാധകമാണ്
ഇംഗ്ലീഷിലെ ഡയമീറ്റർ (diameter) എന്ന പദം, ഗ്രീക്ക് ഭാഷയിലെ ഡയാ (δια, dia, എതിർ)), മെട്രോൺ (μέτρον, metron, അളവ്) എന്നീ പദങ്ങൾ ചേർന്ന ഡയമെട്രോസ് എന്ന പദത്തിൽ നിന്നും വന്നതാണ്.[1]
ഗണിതത്തിൽ വ്യാസം എന്ന പദം വ്യാസരേഖാഖണ്ഡത്തിന്റെ നീളത്തെ സൂചിപ്പിക്കുന്നു. വൃത്തത്തിന്റെയും, ഗോളത്തിന്റെയും വ്യാസം ആരം ആരത്തിന്റെ ഇരട്ടിയാണ്.
ഉത്തലം(convex) ആയ ദ്വിമാനരൂപങ്ങളിൽ, എതിർ വശങ്ങളിലെ സമാന്തരമായ സ്പർശരേഖകൾ തമ്മിലുള്ള കൂടിയ ദൂരത്തെ, വ്യാസം ആയും, കുറഞ്ഞ ദൂരത്തെ ’വീതി’ ആയും കണക്കാക്കുന്നു. റൊട്ടേറ്റിംഗ് കാലിപർ സങ്കേതം ഉപയോഗിച് ഇവ രണ്ടൂം അളക്കാവുന്നതാണ്.[2] റ്യൂല്യാക്സ് ത്രികോണം പോലെയുള്ള പ്രത്യേക തരം ജ്യാമിതീയ രൂപങ്ങളിൽ വീതിയും വ്യാസവും തുല്യമായിരിക്കും
സാമാന്യവത്കരണം
മേൽപറഞ്ഞ നിർവചനങ്ങൾ വൃത്തം, ഗോളം, ഉത്തലം(convex) ആയ ദ്വിമാനരൂപങ്ങൾ എന്നിവക്കു മാത്രം ബാധകമായതാണ്. എന്നാൽ, ഹൈപ്പർ ക്യൂബ് പോലുള്ള, ഉത്തലമോ അപതലമോ ആയ, N-മാനങ്ങളുള്ള ജ്യാമിതീയ രൂപങ്ങൾക്കും, ’ഒരുകൂട്ടം ചിതറിക്കിടക്കുന്ന ബിന്ദുക്കൾക്കും’ ബാധകമായ പൊതുവായ സാമാന്യവത്കൃത നിർവചനവും ഉണ്ട്
ഒരു മെട്രിക് സ്പെയ്സിലെ |ഉപഗണത്തിന്റെ വ്യാസം, ഉപഗണത്തിലെ ബിന്ദു-ജോടികൾ തമ്മിലുള്ള ദൂരത്തിന്റെ ലീസ്റ്റ് അപ്പർ ബൗണ്ട് ആയിരിക്കും. അതായത് ആ ഒരു ഉപഗണം ആണെങ്കിൽ വ്യാസം
- sup { d(x, y) | x, y ∈ A } .
If the distance function d is viewed here as having codomain R (the set of all real numbers), this implies that the diameter of the empty set (the case A = ∅) equals −∞ (negative infinity). Some authors prefer to treat the empty set as a special case, assigning it a diameter equal to 0,[3] which corresponds to taking the codomain of d to be the set of nonnegative reals.
For any solid object or set of scattered points in n-dimensional Euclidean space, the diameter of the object or set is the same as the diameter of its convex hull.
In differential geometry, the diameter is an important global Riemannian invariant.
In plane geometry, a diameter of a conic section is typically defined as any chord which passes through the conic's centre; such diameters are not necessarily of uniform length, except in the case of the circle, which has eccentricity e = 0.
In medical parlance the diameter of a lesion is the longest line segment whose endpoints are within the lesion.
വ്യാസം: ചിഹ്നന സമ്പ്രദായം

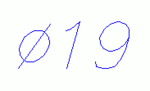
വ്യാസത്തെ സൂചിപ്പിക്കുന്ന ⌀ എന്ന ചിഹ്നം, രൂപത്തിലും വലിപ്പത്തിലും ø എന്ന കുറുകെ വരയോട് കൂടിയ ലാറ്റിൻ ചെറിയ അക്ഷരത്തിന് സമാനമാണ്.
യൂണികോഡിൽ ക്യാരക്ടർ നംപർ 8960(ഹെക്സാഡെസിമൽ 2300), ഈ ചിഹ്നത്തെ കുറിക്കുന്നു.
എച്ച്.ടി.എം.എൽ വെബ് പേജുകളിൽ ഈ ചിഹ്നത്തിനു വേണ്ടി ⌀ അല്ലെങ്കിൽ ⌀ ഉപയോഗിക്കാം.
മൈക്രോസോഫ്റ്റ് വിൻഡോസ് കംപ്യൂട്ടറുകളിൽ ആൾട്ട് കീ അമർത്തിപ്പിടിച്ചുകൊണ്ട് നംബർപാഡിൽ 8960 എന്നു ടൈപ്പ് ചെയ്താൽ മതിയാകും.
ആപ്പിൾ മാകിന്റോഷ് കംപ്യൂട്ടറുകളിൽ വ്യാസ-ചിഹ്നം ലഭിക്കുവാൻ അക്ഷര-പാലറ്റ് (⌥ Opt⌘ CmdT എന്ന് അമർത്തിയാൽ ഇത് തുറക്കാം) ഉപയോഗിക്കാവുന്നതാണ്.
ഇതിനു പകരമായി ø യൂണികോഡിൽ ക്യാരക്ടർ നംപർ 0248(ഹെക്സാഡെസിമൽ 00F8) എന്ന അക്ഷരവും ഉപയോഗിക്കാറുണ്ട്
വ്യാസ-ചിഹ്നം ⌀, ∅ എന്ന ശൂന്യഗണ-ചിഹ്നത്തിൽ നിന്നും, ഫൈ Φ എന്ന ഗ്രീക്-വലിയ അക്ഷരത്തിൽ നിന്നും, നോർദിക് സ്വരാക്ഷരം Ø-ഇൽ നിന്നും വ്യത്യാസപ്പെട്ടിരിക്കുന്നു.[4]
അവലംബം
- ↑ Online Etymology Dictionary
- ↑ Toussaint, Godfried T. (1983). "Solving geometric problems with the rotating calipers". Proc. MELECON '83, Athens.
{{cite journal}}: Cite journal requires|journal=(help) - ↑ Re: diameter of an empty set
- ↑ Korpela, Jukka K. (2006), Unicode Explained, O'Reilly Media, Inc., pp. 23–24, ISBN 978-0-596-10121-3.

