പി വേഴ്സസ് എൻ പി പ്രശ്നം
| കമ്പ്യൂട്ടർ ശാസ്ത്രത്തിലെ പരിഹരിയ്ക്കാനാകാത്ത പ്രശ്നം: ഒരു പ്രശ്നത്തിന്റെ ഉത്തരം ശരിയാണോ എന്ന് എളുപ്പത്തിൽ ഒത്തുനോക്കാൻ പറ്റുമെങ്കിൽ പ്രശ്നം എളുപ്പത്തിൽ പരിഹരിയ്ക്കാൻ സാധിയ്ക്കുമോ?
|

കമ്പ്യൂട്ടർ ശാസ്ത്രത്തിലെ ഇതുവരെ പരിഹരിയ്ക്കാത്ത ഒരു സുപ്രധാനസമസ്യയാണ് പി വേഴ്സസ് എൻ പി പ്രശ്നം. ഏറ്റവും ലഘുവായ ഭാഷയിൽ ഈ പ്രശ്നത്തെ ഇങ്ങനെ എഴുതാം : ഒരു പ്രശ്നത്തിന്റെ തന്നിട്ടുള്ള ഉത്തരം എളുപ്പത്തിൽ ശരിയാണോ എന്ന് പരിശോധിയ്ക്കാൻ സാധിയ്ക്കുമെങ്കിൽ ആ പ്രശ്നം എളുപ്പത്തിൽ പരിഹരിയ്ക്കാൻ സാധിയ്ക്കുമോ? ഇവിടെ 'എളുപ്പത്തിൽ' എന്നതുകൊണ്ട് സാങ്കേതികമായി ബഹുപദ സമയസങ്കീർണതയോടെ ചെയ്യാൻ സാധിയ്ക്കുക എന്നാണ് അർത്ഥമാക്കുന്നത്.
ആദ്യകാല രൂപങ്ങൾ[തിരുത്തുക]
1950 കളിൽ ആണ് ഈ പ്രശ്നം ചർച്ചകളിൽ വന്നു തുടങ്ങിയത്. ജോൺ ഫോർബ്സ് നാഷ് ജൂനിയർ നാഷണൽ സെക്യൂരിറ്റി ഏജൻസിയ്ക്ക് അയച്ച കത്തുകളിലും കുർട് ഗ്വോഡെൽ ജോൺ ഫോൺ ന്യൂമാൻ'ന് അയച്ച കത്തുകളിലും ഈ പ്രശ്നത്തെപ്പറ്റി പരാമർശിച്ചതായി കാണുന്നു. സ്റ്റെഫാൻ കുക്ക് 1971 ൽ പ്രസിദ്ധീകരിച്ച തന്റെ "The complexity of theorem proving procedures" എന്ന പ്രബന്ധത്തിലാണ് ഈ പ്രശ്നത്തിന്റെ കൃത്യമായ നിർവചനം ആദ്യം പുറത്തുവന്നത്.[2] (ലിയോണിഡ് ലെവിൻ 1973-ൽ ഇതിന്റെ നിർവചനം സ്വതന്ത്രമായി പ്രസിദ്ധപ്പെടുത്തിയിരുന്നു.[3]) ഇന്ന് കമ്പ്യൂട്ടർ ശാസ്ത്രത്തിലെ ഏറ്റവും പ്രധാനപ്പെട്ട പരിഹരിയ്ക്കപ്പെടാത്ത സമസ്യയായി ഇതിനെ കണക്കാക്കുന്നു.[4] ക്ലേ മാത്തമാറ്റിക്സ് ഇൻസ്റ്റിറ്റ്യൂട്ട് തെരഞ്ഞെടുത്തിട്ടുള്ള സഹസ്രാബ്ദ പുരസ്കാര സമസ്യകളിൽ ഒന്നാണ് ഇത്. ആദ്യം ഈ പ്രശ്നം പരിഹരിയ്ക്കുന്നയാൾക്ക് ഒരു ദശലക്ഷം ഡോളറിന്റെ സമ്മാനത്തുകയും അവർ പ്രഖ്യാപിച്ചിട്ടുണ്ട്.
വിവരണം[തിരുത്തുക]
മുകളിൽ കൊടുത്തിട്ടുള്ള എളുപ്പത്തിൽ എന്ന വാക്ക് കുറച്ചുകൂടി വിശദീകരിയ്ക്കണം. തന്നിട്ടുള്ള ഒരു പണി എളുപ്പത്തിൽ പൂർത്തിയാക്കുക എന്നാൽ ആ പണി ചെയ്യാൻ ബഹുപദ (polynomial) സമയസങ്കീർണതയുള്ള ഒരു വഴി (അൽഗോരിതം) ഉണ്ടെന്നാണ് ഇതിന്റെ അർത്ഥം. ബഹുപദം എളുപ്പമാണെങ്കിൽ എന്താണ് കഠിനം? ഈ പ്രശ്നം ചർച്ച ചെയ്യുന്ന ചുറ്റുപാടിൽ ഉളവാകുന്ന മറ്റൊരു സങ്കീർണതാ ടൈപ്പ് എക്സ്പോണെൻഷ്യൽ സങ്കീർണതയാണ്. അത്തരം പ്രശ്നങ്ങളെ കഠിനമായ പ്രശ്നങ്ങൾ എന്നു വിളിയ്ക്കുന്നു. ബഹുപദസങ്കീർണതയോടെ പരിഹരിയ്ക്കാൻ സാധിയ്ക്കുന്ന പ്രശ്നങ്ങളുടെ ഗണത്തെ P ക്ലാസ് അഥവാ P ടൈപ്പ് പ്രശ്നങ്ങൾ എന്ന് വിളിയ്ക്കുന്നു. എന്നാൽ ഇത്തരത്തിൽ ബഹുപദ സങ്കീർണതയോടെ പരിഹരിയ്ക്കാൻ സാധിയ്ക്കാത്ത ചില പ്രശ്നങ്ങൾ ഉണ്ട്. ഇവയിൽ (കഠിനപ്രശ്നങ്ങളിൽ ചിലതിനെ, എല്ലാത്തിനെയും അല്ല) ചിലതിന്റെ ഉത്തരങ്ങൾ കിട്ടിയാൽ അവ ശരിയാണോ എന്ന് ബഹുപദ സങ്കീർണതയോടെ തന്നെ ഒത്തു നോക്കാൻ കഴിഞ്ഞേക്കും. അതായത് ചില കഠിന പ്രശ്നങ്ങളുടെ ഉത്തരങ്ങൾ ശരിയാണോ എന്ന് നോക്കൽ എളുപ്പമാണ്. ഇത്തരം പ്രശ്നങ്ങളുടെ ഗണത്തെ NP ക്ലാസ് പ്രശ്നങ്ങൾ എന്ന് വിളിയ്ക്കുന്നു. നോൺ-ഡിറ്റർമിനിസ്റ്റിക് പോളിനോമിയൽ ടൈം എന്നാണ് NP എന്നതിന്റെ മുഴുവൻ രൂപം.[Note 1]
സുഡോകു കളി ഉദാഹരണമായി എടുക്കുക. ഒരു സുഡോകു ബോർഡിൽ വിവിധ സംഖ്യകൾ നിറച്ച് ആരെങ്കിലും തന്നാൽ അത് ശരിയാണോ എന്ന് നമുക്ക് എളുപ്പത്തിൽ പരിശോധിയ്ക്കാം. ഓരോരോ വരിയും നിരയും പരിഗണിച്ചു അവയിലെ അക്കങ്ങൾ എല്ലാം പത്തിൽ താഴെ ആണെന്നും അവ ഒന്നും തന്നെ ആവർത്തിയ്ക്കുന്നില്ല എന്ന് കണ്ടെത്തിയാൽ മതി. എത്ര വരിയും നിരയുമുണ്ടോ അത്രയ്ക്കും ചെക്കുകൾ നടത്തിയാൽ മാത്രം മതി. അതായത് ഒരു സുഡോക്കുവിന്റെ ഉത്തരം ശരിയാണോ എന്ന് ചെക്ക് ചെയ്യാനുള്ള അൽഗോരിതത്തിന്റെ സമയ സങ്കീർണത സുഡോകു കളത്തിന്റെ വലിപ്പത്തിന് രേഖീയ അനുപാതത്തിൽ ആണ്. എന്നാൽ ഇത്തരം ഒരു ബോർഡ് തന്നാൽ അതിന്റെ ശരിയായ ഉത്തരം കണ്ടുപിടിയ്ക്കാനുള്ള ഏറ്റവും മികച്ച അൽഗോരിതം പോലും എക്സ്പോണെൻഷ്യൽ സമയം എടുക്കും. അതായത് സുഡോകു ഇപ്പോൾ NP ക്ലാസ്സിൽ പെട്ട ഒരു പ്രശ്നമാണ് (പരിഹരിയ്ക്കാൻ കഠിനം, എന്നാൽ ഉത്തരം കിട്ടിയാൽ ശരിയാണോ എന്ന് നോക്കാൻ എളുപ്പം). ഇത് ഇപ്പോൾ P ക്ലാസ്സിൽ പെടുന്നില്ല.
ഇത്തരത്തിൽ എളുപ്പത്തിൽ ഉത്തരം ചെക്ക് ചെയ്യാൻ പറ്റുന്ന, എന്നാൽ എളുപ്പത്തിൽ പരിഹരിയ്ക്കാൻ പറ്റാത്ത ആയിരക്കണക്കിന് പ്രശ്നങ്ങൾ ഉണ്ട്. എന്നാൽ ഇതിൽ ഇത്തരം പ്രശ്നങ്ങളിൽ ഏതെങ്കിലും ഒന്നിനെ എളുപ്പത്തിൽ പരിഹരിയ്ക്കാൻ കഴിഞ്ഞാൽ ഈ ഗണത്തിലെ മറ്റെല്ലാ പ്രശ്നങ്ങളെയും എളുപ്പത്തിൽ പരിഹരിയ്ക്കാൻ സാധിയ്ക്കും എന്ന ഗവേഷകർ കണ്ടെത്തിയിട്ടുണ്ട്. ഈ പ്രത്യേകതയെ NP കമ്പ്ലീറ്റ്നെസ് എന്ന് വിളിയ്ക്കുന്നു. ദശാബ്ദങ്ങളായി ഇവയ്ക്ക് ബഹുപദ സങ്കീർണതയുള്ള അൽഗോരിതങ്ങൾ കണ്ടെത്താൻ ശ്രമം നടക്കുന്നുണ്ടെങ്കിലും ഇതു വരെ ഒന്നും കണ്ടെത്തിയിട്ടില്ല. അതിനാൽ ഇത്തരം അൽഗോരിതങ്ങൾ കണ്ടെത്താൻ സാധ്യമല്ല എന്ന് ശാസ്ത്രജ്ഞർ വിശ്വസിയ്ക്കുന്നു. എന്നാൽ സാധ്യമല്ല എന്ന് തെളിയിയ്ക്കപ്പെട്ടിട്ടില്ല.
മുകളിൽ കൊടുത്തിട്ടുള്ള വിവരണത്തിൽ നിന്നും P ക്ലാസ് പ്രശ്നങ്ങൾ എല്ലാം തന്നെ NP പ്രശ്നങ്ങൾ തന്നെയാണെന്ന് കാണാം. അതായത് ബഹുപദ സങ്കീർണതയുള്ള പ്രശ്നങ്ങളുടെ ഉത്തരങ്ങൾ എല്ലാം തന്നെ ബഹുപദ സങ്കീർണതയോടെ തന്നെ ഒത്തുനോക്കാൻ സാധിയ്ക്കുമല്ലോ. എന്നാൽ എല്ലാ NP പ്രശ്നങ്ങളും ഇപ്പോഴത്തെ അറിവ് വെച്ച് P ക്ലാസ്സിൽ പെടുന്നില്ല. ഇതിനെ ഗണിതശാസ്ത്രപരമായി ഇങ്ങനെ എഴുതാം.
P ⊆ NP -> ഇത് നമുക്കറിയാം
NP ⊆ P -> ഇത് നമുക്കറിയില്ല
ഗണസിദ്ധാന്തത്തിൽ രണ്ടു ഗണങ്ങൾ തുല്യമാകണമെങ്കിൽ ഈ രണ്ടു ഉപഗണബന്ധങ്ങളും സത്യവാക്യം ആയിരിയ്ക്കണം. ഈ രണ്ടു ബന്ധങ്ങളെയും അനുബന്ധമായ ചോദ്യത്തെയും ചുരുക്കി ഇങ്ങനെ സൂചിപ്പിയ്ക്കുന്നു:
P = NP?
ഇതാണ് പി വേഴ്സസ് എൻ പി പ്രശ്നം എന്നറിയപ്പെടുന്നത്.
P = NP? എന്ന പ്രശ്നത്തിന് അതേ എന്നാണ് ഉത്തരം എങ്കിൽ സുഡോകു പോലുള്ള പ്രശ്നങ്ങൾ പരിഹരിയ്ക്കാനുള്ള ബഹുപദ സങ്കീർണതയുള്ള അൽഗോരിതങ്ങൾ ലഭിയ്ക്കും. അല്ല എന്നാണെങ്കിൽ ഇത്തരം പ്രശ്നങ്ങൾ ഒരിയ്ക്കലും എളുപ്പത്തിൽ പരിഹരിയ്ക്കാൻ പറ്റില്ല എന്ന് മനസ്സിലാക്കാൻ സാധിയ്ക്കും.
അനന്തരഫലങ്ങൾ[തിരുത്തുക]
ഈ പ്രശ്നത്തിന്റെ ശരിയായ ഒരു തെളിവ് ഗണിതം, ക്രിപ്ടോഗ്രഫി, അൽഗോരിതഗവേഷണം, നിർമിത ബുദ്ധി, ഗെയിം തിയറി, മൾട്ടിമീഡിയ പ്രോസസ്സിംഗ്, തത്ത്വശാസ്ത്രം, സാമ്പത്തികശാസ്ത്രം തുടങ്ങിയ പല മേഖലകളിലും ദൂരവ്യാപകമായ ഫലങ്ങൾ ഉളവാക്കും.[5]
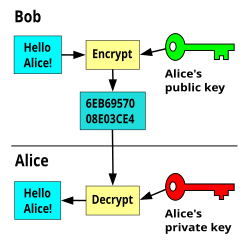
ഇന്റർനെറ്റ് സുരക്ഷയുടെ ആണിക്കല്ലായ പല ക്രിപ്റ്റോഗ്രഫിക് അൽഗോരിതങ്ങളും ചില ഗണിതപ്രശ്നങ്ങൾ പരിഹരിയ്ക്കാൻ എക്സ്പോണെൻഷ്യൽ സമയം വേണമെന്ന പൊതുധാരണയിലാണ് എഴുതപ്പെട്ടിരിയ്ക്കുന്നത്. ഇത്തരം അൽഗോരിതങ്ങളിൽ ഉപയോഗിയ്ക്കപ്പെടുന്ന ഒരു സങ്കേതമാണ് പൂർണസംഖ്യകളുടെ ഘടകക്രിയ.[6][7] ഉദാഹരണത്തിന് 35 എന്ന ഒരു സംഖ്യ കിട്ടിയാൽ അത് 7, 5 എന്നീ അഭാജ്യസംഖ്യകളുടെ ഗുണിതമാണ് എന്ന് നമുക്ക് കണ്ടുപിടിയ്ക്കാം. പബ്ലിക് കീ ഇൻഫ്രാസ്ട്രക്ചർ എന്ന ക്രിപ്റ്റോഗ്രഫിക് സങ്കേതത്തിൽ രഹസ്യമായി അയയ്ക്കേണ്ട ഡാറ്റയെ ഒരു പബ്ലിക് കീ (അടയ്ക്കാനുള്ള താക്കോൽ; ലഘുവായ ഒരു ഉദാഹരണത്തിൽ 35 എന്ന ഗുണിതം) ഉപയോഗിച്ച് എൻകോഡ് ചെയ്ത് അയയ്ക്കുന്നു (ഇത് പേര് സൂചിപ്പിയ്ക്കുന്ന പോലെ തന്നെ എല്ലാവരുടെ അടുത്തും കാണും. ഇത് വെച്ച് ആർക്കും ഡാറ്റ എൻകോഡ് ചെയ്യാം). ഇതിന്റെ ഒരു അഭാജ്യഘടകമായ 5 എന്ന നമ്പർ ആയിരിയ്ക്കും ഈ സ്കീമിലെ പ്രൈവറ്റ് കീ(തുറക്കാനുള്ള താക്കോൽ). ഈ പ്രൈവറ്റ് കീ വിവരം സ്വീകരിയ്ക്കുന്ന ആളുടെ അടുത്ത് മാത്രമേ കാണൂ. അയാൾക്ക് ഈ പ്രൈവറ്റ് കീ ഉപയോഗിച്ച് ഡാറ്റ ഡീകോഡ് ചെയ്തു എടുക്കാവുന്നതാണ്. ഈ ഉദാഹരണത്തിൽ പ്രൈവറ്റ് കീ കൈയിൽ ഇല്ലാത്ത മൂന്നാമതൊരാൾക്ക് 35 എന്ന പബ്ലിക് കീ അറിഞ്ഞാൽ തന്നെയും പ്രൈവറ്റ് കീ കണ്ടുപിടിയ്ക്കണമെങ്കിൽ പബ്ലിക് കീയെ ഘടകക്രിയ ചെയ്തു നോക്കേണ്ടി വരും. 35 എന്ന സംഖ്യയുടെ ഘടകക്രിയ ചെയ്യണമെങ്കിൽ 1 മുതൽ 6 വരെയുള്ള ഓരോ സംഖ്യകൾ കൊണ്ടും 35 നെ ഹരിച്ചു നോക്കേണ്ടി വരുമല്ലോ. ചെറിയ സംഖ്യകൾക്ക് ഇത് എളുപ്പമാണെങ്കിലും സംഖ്യ വലുതാകും തോറും ഈ പ്രക്രിയ വളരെയേറെ സമയമെടുക്കുന്ന ഒന്നായി മാറും. നൂറുകണക്കിന് അക്കങ്ങളുള്ള കീകൾ ആണ് ആണ് സാധാരണയായി എൻകോഡിങ്ങിന് ഉപയോഗിയ്ക്കുന്നത്. ഇവയുടെ ഘടകക്രിയ ചെയ്തു ഒരു ഘടകം കണ്ടെത്താൻ അനേകദശലക്ഷം വർഷങ്ങൾ വേണ്ടി വരും. എന്നാൽ P = NP എന്നത് ശരിയാണെന്ന് തെളിഞ്ഞാൽ ഈ ഘടകക്രിയ ചെയ്തുതീർക്കാൻ പെട്ടെന്ന് കഴിഞ്ഞെന്ന് വരും. അതോടെ ഇത്തരം സങ്കേതങ്ങളിൽ അധിഷ്ഠിതമായ ക്രിപ്റ്റോഗ്രഫി മാറ്റിയെഴുതേണ്ടി വരും.[8][9][10]
തെളിവിനുള്ള ശ്രമങ്ങൾ[തിരുത്തുക]
ഈ പ്രശ്നം ഇന്നുവരെ കുറ്റമറ്റ രീതിയിൽ ആരും തെളിയിച്ചിട്ടില്ല എന്ന് കരുതപ്പെടുന്നു.[11]
ഗണിത/കമ്പ്യൂട്ടർ ശാസ്ത്രത്തിലെ സുപ്രധാന പ്രശ്നമായതിനാൽ വളരെയേറെപ്പേർ കാലങ്ങളായി ഇതിന്റെ തെളിവിനായി ശ്രമിയ്ക്കുന്നുണ്ട്. അതിനാൽ ധാരാളം തെളിവുകൾ പ്രസിദ്ധീകരിയ്ക്കപ്പെട്ടിട്ടുണ്ട്. ഇവയിൽ പലതും പിൽക്കാലത്ത് തെറ്റാണെന്ന് തെളിയിയ്ക്കപ്പെട്ടു. ഗെർഹാർഡ് വോയ്ഗിംഗർ എന്ന ഗണിതശാസ്ത്രജ്ഞൻ സൂക്ഷിച്ചിരിയ്ക്കുന്ന ഒരു ലിസ്റ്റ് പ്രകാരം 2018ൽ P = NP ആണെന്ന് സ്ഥാപിയ്ക്കുന്ന 62 തെളിവുകളും P ≠ NP ആണെന്ന് സ്ഥാപിയ്ക്കുന്ന 50 തെളിവുകളും പ്രൂവ് ചെയ്യാൻ പറ്റില്ല എന്ന് സ്ഥാപിയ്ക്കുന്ന രണ്ടു തെളിവുകളും തീരുമാനിയ്ക്കാനേ പറ്റില്ല എന്ന് സ്ഥാപിയ്ക്കുന്ന ഒരു തെളിവും ഉണ്ട്.[12]
2010 ഓഗസ്റ്റിൽ വിനയ് ദിയോലാലികർ എന്ന ഗണിതശാസ്ത്രജ്ഞൻ P ≠ NP ആണെന്ന് സ്ഥാപിയ്ക്കുന്ന ഒരു തെളിവ് പ്രസിദ്ധീകരിച്ചത് ശാസ്ത്രശ്രദ്ധ പിടിച്ചുപറ്റിയിരുന്നു.[13] പല അക്കാഡമികളും ഈ തെളിവ് കാര്യമായെടുത്ത് തുടർപരിശോധനകൾ നടത്തിയിരുന്നു.[14][15] എന്നാൽ ഈ തെളിവ് ശരിയല്ല എന്ന നിഗമനത്തിലാണ് പൊതുവെ എല്ലാവരും എത്തിച്ചേർന്നത്.[16] ദിയോലാലികർ തന്റെ തെളിവിനെ ശരിയാക്കാനായി കൂടുതൽ പരിശ്രമിച്ചെങ്കിലും അദ്ദേഹം ഉപയോഗിച്ച സങ്കേതങ്ങൾ വെച്ച് ഈ പ്രശ്നം പരിഹരിയ്ക്കാനാകില്ല എന്നായിരുന്നു പൊതുവെയുള്ള അഭിപ്രായം.[17][18] 2013 മെയ് മാസത്തിൽ ദി ന്യൂ യോർക്കർ പത്രത്തിൽ പ്രസിദ്ധീകരിയ്ക്കപ്പെട്ട വിശദമായ ഒരു ലേഖനത്തിൽ ഈ തെളിവ് ശരിയല്ല എന്ന് സംശയാതീതമായി തെളിയിയ്ക്കപ്പെട്ടു എന്ന് രേഖപ്പെടുത്തിയിട്ടുണ്ട്.[19]
കുറിപ്പുകൾ[തിരുത്തുക]
- ↑ A nondeterministic Turing machine can move to a state that is not determined by the previous state. Such a machine could solve a NP problem in polynomial time by falling into the correct answer state (by luck), then conventionally verifying it. Such machines are not practical for solving realistic problems but can be used as theoretical models.
അവലംബങ്ങൾ[തിരുത്തുക]
- ↑ R. E. Ladner "On the structure of polynomial time reducibility," Journal of the ACM 22, pp. 151–171, 1975. Corollary 1.1. ACM site.
- ↑ Cook, Stephen (1971). "The complexity of theorem proving procedures". Proceedings of the Third Annual ACM Symposium on Theory of Computing. pp. 151–158.
- ↑ L. A. Levin (1973). "Универсальные задачи перебора" (in റഷ്യൻ). 9 (Problems of Information Transmission ed.): 115–116.
{{cite journal}}: Cite journal requires|journal=(help)CS1 maint: date and year (link) - ↑ Fortnow, Lance (2009). "The status of the P versus NP problem" (PDF). Communications of the ACM. 52 (9): 78–86. doi:10.1145/1562164.1562186.
- ↑ Fortnow, Lance (2013). The Golden Ticket: P, NP, and the Search for the Impossible. Princeton, NJ: Princeton University Press. ISBN 9780691156491.
- ↑ Krantz, Steven G. (2011), The Proof is in the Pudding: The Changing Nature of Mathematical Proof, New York: Springer, p. 203, doi:10.1007/978-0-387-48744-1, ISBN 978-0-387-48908-7, MR 2789493
- ↑ Arora, Sanjeev; Barak, Boaz (2009), Computational complexity, Cambridge: Cambridge University Press, p. 230, doi:10.1017/CBO9780511804090, ISBN 978-0-521-42426-4, MR 2500087
- ↑ See Horie, S. and Watanabe, O.; Watanabe (1997). Hard instance generation for SAT. Lecture Notes in Computer Science. Vol. 1350. Springer. pp. 22–31. arXiv:cs/9809117. Bibcode:1998cs........9117H. doi:10.1007/3-540-63890-3_4. ISBN 978-3-540-63890-2.
{{cite book}}:|journal=ignored (help)CS1 maint: multiple names: authors list (link) for a reduction of factoring to SAT. A 512 bit factoring problem (8400 MIPS-years when factored) translates to a SAT problem of 63,652 variables and 406,860 clauses. - ↑ See, for example, Massacci, F.; Marraro, L. (2000). "Logical cryptanalysis as a SAT problem". Journal of Automated Reasoning. 24 (1): 165–203. CiteSeerX 10.1.1.104.962. doi:10.1023/A:1006326723002.
{{cite journal}}: Unknown parameter|lastauthoramp=ignored (|name-list-style=suggested) (help) in which an instance of DES is encoded as a SAT problem with 10336 variables and 61935 clauses. A 3DES problem instance would be about 3 times this size. - ↑ De, Debapratim and Kumarasubramanian, Abishek and Venkatesan, Ramarathnam (2007). "Inversion attacks on secure hash functions using SAT solvers". Springer. pp. 377–382. doi:10.1007/978-3-540-72788-0_36.
{{cite news}}: Unknown parameter|booktitle=ignored (help)CS1 maint: multiple names: authors list (link) - ↑ John Markoff (8 October 2009). "Prizes Aside, the P-NP Puzzler Has Consequences". The New York Times.
- ↑ Gerhard J. Woeginger. "The P-versus-NP page". Retrieved 2018-06-24.
- ↑ Markoff, John (16 August 2010). "Step 1: Post Elusive Proof. Step 2: Watch Fireworks". The New York Times. Retrieved 20 September 2010.
- ↑ Polymath Project wiki. "Deolalikar's P vs NP paper".
- ↑ Science News, "Crowdsourcing peer review"
- ↑ Dick Lipton (12 August 2010). "Fatal Flaws in Deolalikar's Proof?".
- ↑ Dick Lipton (15 September 2010). "An Update on Vinay Deolalikar's Proof". Retrieved 31 December 2010.
- ↑ Gödel’s Lost Letter and P=NP, Update on Deolalikar’s Proof that P≠NP
- ↑ Alexander Nazaryan (2 May 2013). "A Most Profound Math Problem". Retrieved 1 May 2014.
കൂടുതൽ വായനയ്ക്ക്[തിരുത്തുക]
- Fraenkel, A. S.; Lichtenstein, D. (1981). "Computing a Perfect Strategy for n*n Chess Requires Time Exponential in N." Lecture Notes in Computer Science: 278–293. doi:10.1007/3-540-10843-2_23. Archived from the original on 2017-04-25.
- Garey, Michael; Johnson, David (1979). Computers and Intractability: A Guide to the Theory of NP-Completeness. San Francisco: W. H. Freeman and Company. ISBN 0-7167-1045-5.
- Goldreich, Oded (2010). P, Np, and Np-Completeness. Cambridge: Cambridge University Press. ISBN 978-0-521-12254-2. Online drafts
- Immerman, N. (1987). "Languages which capture complexity classes". SIAM Journal on Computing. 16 (4): 760–778. CiteSeerX 10.1.1.75.3035. doi:10.1137/0216051.
- Cormen, Thomas (2001). Introduction to Algorithms. Cambridge: MIT Press. ISBN 0-262-03293-7.
- Papadimitriou, Christos (1994). Computational Complexity. Boston: Addison-Wesley. ISBN 0-201-53082-1.
- Fortnow, L. (2009). "The Status of the P versus NP problem". Communications of the ACM. 52 (9): 78. doi:10.1145/1562164.1562186.
- Fortnow, L.; Gasarch, W. "Computational complexity".
പുറംകണ്ണികൾ[തിരുത്തുക]
- The Clay Mathematics Institute Millennium Prize Problems
- "The Clay Math Institute Official Problem Description" (PDF). Archived from the original (PDF) on 2015-09-04. Retrieved 2018-06-16. (118 KB)
- Gerhard J. Woeginger. The P-versus-NP page. A list of links to a number of purported solutions to the problem. Some of these links state that P equals NP, some of them state the opposite. It is probable that all these alleged solutions are incorrect.
- Scott Aaronson 's Shtetl Optimized blog: Reasons to believe, a list of justifications for the belief that P ≠ NP
- Aviad Rubinstein's Hardness of Approximation Between P and NP, winner of the ACM's 2017 Doctoral Dissertation Award.
