ഋണസംഖ്യ
പൂജ്യത്തിൽ കുറവായ വാസ്തവികസംഖ്യകളെ ഋണസംഖ്യ എന്ന് പറയുന്നു.നഷ്ടത്തിന്റെയോ അസാന്നിദ്ധ്യത്തിന്റെയോ അളവ് സൂചിപ്പിക്കാനാണ് ഇവ മിക്കപ്പോഴും ഉപയോഗിക്കുന്നത്. ഉദാഹരണത്തിന് കടത്തെ ഋണസംഖ്യയാൽ കുറിക്കുന്ന മുതലായി കണക്കാക്കാം,എന്തിന്റെയെങ്കിലും അളവിലുണ്ടാകുന്ന കുറവിനെ ഋണസംഖ്യകൊണ്ട് കുറിക്കുന്ന വർദ്ധനയായി കണക്കാക്കാം. ഋണസംഖ്യയാണെന്ന് സൂചിപ്പിക്കാൻ സംഖ്യക്കു മുൻപിൽ ഒരു ഋണ ചിഹ്നം ഇടുന്നു. ഉദാ -128. പൂജ്യം ഒരു ഋണസംഖ്യയോ ധനസംഖ്യയോ അല്ല. താഴെക്കാണുന്ന വാസ്തവികസംഖ്യരേഖ ഋണസംഖ്യ, പൂജ്യം, ധനസംഖ്യ എന്നിവ തമ്മിലുള്ള ബന്ധത്തെ കാണിക്കുന്നു.
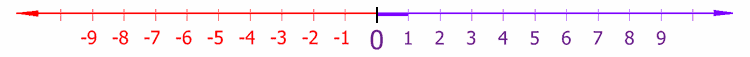
ഋണസംഖ്യയുടെ സ്വഭാവഗുണങ്ങൾ (properties of negative numbers)[തിരുത്തുക]
- ഒരു സംഖ്യയിൽ നിന്ന് ഒരു ഋണസംഖ്യ വ്യവകലനം ചെയ്യുമ്പോൾ അത് ഫലത്തിൽ സങ്കലനമാവുന്നു ഉദാ : (+8) - (-2) = (+10).
- ഒരു ഋണസംഖ്യയും ധനസംഖ്യയുമായുള്ള ഗുണിക്കുമ്പോൾ കിട്ടുന്നഫലം ഋണസംഖ്യയായിരിക്കും ഉദാ : (+8) x (-2) = (-16)
- ഋണസംഖ്യകൾ മറ്റൊരു സംഖ്യയുമായി ഹരണം ചെയ്യുമ്പോൾ ഫലം ഋണമായിരിക്കും ഉദാ : (+8) ÷ (-2) = (-4)
അവലംബം[തിരുത്തുക]
- Bourbaki, Nicolas (1998). Elements of the History of Mathematics. Berlin, Heidelberg, and New York: Springer-Verlag. ISBN 3-540-64767-8.
- Struik, Dirk J. (1987). A Concise History of Mathematics. New York: Dover Publications.
